Carntine loss
Valporate Carnitine
Heart and Carnitine
Felice Perine Carntine
Colon cancer Carntine
CrP colon cancer risk biomarker
Sunday, 1 September 2013
Monday, 26 August 2013
LED Red 633 nm
from heelspur verbatim
This article has been around for years and I'm constantly updating it. Here are 3 errors in previous editions that are mostly corrected in this edition:
LED Light Device

Red and near-infrared light are a "window" of wavelengths that are able
to pass through tissue up to 1 inch deep (not 6 inches like some web
sites claim). Red and near-infrared have beneficial effects on cells
by "kick-starting" them into immediately creating more ATP (cellular
energy) and increasing DNA and RNA activity. This effect has been
carefully studied in many published reports since 1987. The positive
effects occur only in injured cells. There is probably not much
benefit to healthy cells. In the past, lasers were thought to be needed
to provide the light, but it's been known since 1989 that LEDs are just
as good. The ideal wavelengths are between 600 and and 900 nm, with
the best results at specific ranges: 610-625, 660-690, 750-770, and
815-860 nm (see below).
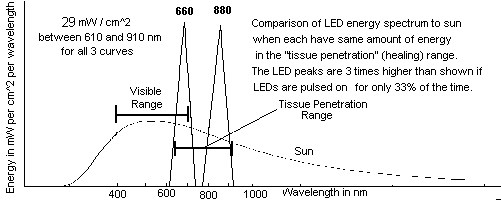
LED light arrays are a means to provide these wavelengths. Companies may claim lasers and pulse rates are important, but the only things are the wavelength and total amount of light energy applied. For example, 880 nm is a bad choice. Bright noon-time summer Sun only has half as much light energy as LED devices in the optimum wavelengths, but it covers the entire body (which is good for fibromyalgia). The advantages of LEDs over sunlight are: 1) LEDs can be applied at any time, 2) LEDs require only one hour instead of two hours for injuries beneath the skin, 3) LEDs don't cause sunburn.
Halogen lights emit a spectrum of light that is very similar to sunlight (see this chart or this). Like bright sun, halogen provides an inexpensive source of "healing light energy" in the 600 to 900 nm wavelengths (see Halogen Lights section below), but the energy is not concentrated at the best wavelengths as in LEDs. My interest in light therapy increased a great deal when a halogen treatment returned my black-and-blue broken small toe to almost a normal color in 5 minutes. Pain level went from 8 to 2. I repeated the treatment 6 hours later when the toe turned blue and painful again and received the same benefits.
Heat lamps have long been used to reduce pain. It was believed the heat provided a benefit, but now we know the near-infrared portion of the spectrum of heat lamps provides more benefit than the heat of the far-infrared.

How useful is light therapy? I view red and infrared light as equally beneficial regardless of the source (sun, halogen, LED, or laser) as long as the intensity and area of coverage are equal. I think 830 nm is best, but maybe 660 nm is better, and in either case, you can just make the less beneficial wavelength have a stronger light source. There is no theory that indicates the effects are different. They kick-start injured cells into making more ATP. I view red/near-infrared light therapy as beneficial overall as applying ice to injuries, keeping in mind that people greatly under-utilize ice. More important than ice and light for joint injuries is a lot of stretching, movement, and careful strengthening. I use light mostly immediately after an injury, right before applying ice for 5 minutes, and then repeat once every 6 hours for a day or two. Immediately after injuries, ice is more important.
FDA allows advertising red and infrared for minor pains and mild arthritis. Red has been used to help halt dry macular degeneration which may have FDA approval. The following have FDA approval for specific devices (these are just those I know. I have not done a search): infrared 880 nm for diabetic peripheral neuropathy, 660 nm red for mouth ulcers in children on a type of chemo, "Titan" intense infrared device for wrinkles in a clinical setting, very intense (harmful) infrared devices for spots, and blue or blue/red for acne. There have been excellent results reported for tendonitis, shoulders, knees, small joints, and fibromyalgia. For most soft-tissue injuries beneath the skin, the pain goes from an 8 to a 2 (on a scale of 10) after an hour or two of treatment with good home-use LED devices. For exposed injuries like burns and retina injuries, only 1 to 10 minutes of LED light is used, depending on the device. Applying LED light for too long cancels the benefits, but the time of application is hard to determine. Too little light and there is little benefit, and too much light and there is no benefit. For injuries where the pain can be felt, I apply it only long enough to notice the maximum pain relief and no longer. The pain relief can be amazing in burns, cuts, and other wounds even if wound healing is not faster. The increase in the speed of healing can be directly measured in the injured retinas of rabbit. Stubbed toes can go from being purple-black to pink in one treatment. Serious injuries seem to benefit from 3 to 6 treatments/day (as the pain returns) instead of one treatment/day. Strangely, tendon and muscle soreness from working-out seems to not receive any pain relief, but chronic tendinitis seems to benefit greatly. From my experience in trying to help friends and family, it is beneficial only about 30% of the time in back pain. Companies have made various strange claims that I do not believe: yellow for wrinkles, green for cancer, and blue for wrinkles. Recent serious injuries benefit from several treatments per day.
In hindsight, we can say "people have always known Sunlight is good for you". It seems intuitively clear to most people that Sunlight helps sick people and enables people to be more active. We know why from a chemical and biological viewpoint. Injured cells need the extra ATP to repair themselves. Healthy cells may generate extra ATP from the red and near infrared of sunlight to enable more activity in the daytime. If the ATP is not used (as occurs when resting in bright sunlight) it causes an increase in available glucose for which causes a slight "glucose high" that causes relaxation and sleepiness we all feel after 30 minutes in the sun. BTW, we know UV creates vitamin D that prevents colon, prostate, and breast cancer, greatly improves the immune system, bone strength, and reduces the incidence of osteoarthritis, having the potential to save 50,000 lives a year if people would get more Sun and wear less sunscreen. By comparison, skin cancer causes less than 10,000 deaths in the U.S. each year, only some of which are caused by too much Sun.
Evolution Theory Support: There are 5 indications that the benefit of red and near-infrared light is not an accident, but a highly "intelligent" and natural result of evolution. The indications are: 1) The proton pump is the last in a series of 3 pumps which places it in possibly the best location to pull the food conversion process along by "pushing" the final electrons through the chain. This creates electrostatic pull on the electrons further back in the chain. 2) The pump absorbs primarily the red and near-infrared light and the remaining sunlight wavelengths are blocked by water and blood. 3) The pump is the primary absorber of these wavelengths in the body, very roughly about 35%. 4) Oxygenated hemoglobin has a very sharp decline in it's ability to absorb red and near-infrared which indicates hemoglobin evolved specifically to allow these wavelengths to pass through. The CCO pump has a longer evolutionary history than hemoglobin because it was inherited from bacteria that formed the symbiotic relationship in mitochondria. Decendents of these bacteria still exist as purple bacteria which are used in most research on the CCO pump. 5) Night-time levels of melatonin, but not day-time levels, have been shown by Tiina Karu to completely inhibit the positive effects of infrared light. This indicates that melatonin and its wide swings over 24 hours could have evolved to not inhibit the benefits of sunlight.
In the "test tube", antioxidants nagate the effects of the light, and the light negates the effects of oxidants. In some sense, this may be like the light is an antioxidant.
Details on cytochrome c oxidase: As the CCO absorbs light, its two copper atoms are either oxidized or reduced to transport electrons that are required to help pump H+ to increase the gradient that allows for more ATP. This increases respiration (krebs cycle molecules provide the energy). Calcium Ca2+, alkalinity (0.2 units), and oxidation are increased which causes important secondary responses such as transcription factors that increase DNA and RNA activity. The creation of more ATP increases respiration that increases the production of O-2 oxidation which can be harmful if too much light is applied. Daily moderate use of light therapy induces up-regulation of antioxidants like MnSOD to counteract the harmful oxidation of O2- in a manner much like moderate exercise. Light therapy increases NAD+ which is known to increase endurance as well as increase MnSOD. Over the short-term, heavy exercise depletes NAD+ but light exercise increases it (reference). Light therapy increases GSH (glutathione) which decreases H2O2 that is produced from the extra MnSOD that is converting O-2 to H2O2. Too much wide-spectrum infrared light, such as that received from 3 hours of bright sunlight, causes too much H2O2 which will increase MMP-1 (at least in the dermis of the skin) which some researchers think could cause photo-aging, but not cancer.
By creating an "electron drain" in complex IV (CCO), super oxide O2- may be decreased directly by an electrostatic pull on cytochrome c and thereby on complex III, preventing electron leakage that is believed to result in super oxide O2-. Similar reasoning in the may also indicate an excess of light can actually cause free radicals. The chemical NO is prevented from halting CCO activity and this may explain the immediate pain relief. More electrons being transported to create ATP oxidizes ("alkalinizes") the entire mitochondria, increasing the ratios NAD+/NADH, NADP+/NADPH, GSH/GSSG and signaling important secondary effects such as transcription factors which signal more DNA and RNA. The idea that 600 to 900 nm wavelengths activate cytochrome c oxidase was first proposed 20 years ago by Tiina Karu in 1988. See her 2003 great summary for more about light therapy and CCO.
CCO absorbs energy from 600-900 nm (2.8 eV) photons and reflects them individually with a slightly longer wavelength (approx 50 nm longer), extracting about 0.1 eV of energy in assisting the 0.80 eV (not 0.43 eV) released from a molecule of ATP. If CCO in the body is able to absorb 5% of the 1E17 photons/cm^2 (30 mW/cm^2) in the 600-900 nm range from bright Sun over 0.5 m^2 of skin for 4 hours, then the body has gained 0.030*0.05*5000 cm^2 * 0.1/2.8 = 0.27 watts while using about 100 watts during those 4 hours (0.9 kcalories), making us 0.27% photosynthetic during those 4 hours. The light is directly photo-assisting in the creation of the ATP chemical energy. This does not include the calories absorbed from light that reduces the need for maintaining body temperature.

Our ancestors have been exposed to 0.01 to 0.03 W/cm^2 of sunlight in the red to near-infrared range for up to 6 hours a day, giving an average daily dosage in the hundreds of J/cm^2 for very large areas of skin. People with fibromyalgia and arthritis will not a large reduction in pain when the painful areas are exposed to sunlight for a long time. This is strong support for the idea that 1,000 J/cm^2 is not unreasonable in a clinical setting for > 1 inch deep injuries that occur from trauma or surgery. I have found 100 J/cm^2 to reduce pains that are about 1/2 inch deep from an pain level of 8 to 2. I have not observed any harm from 30 minutes of 150 mW/cm^2 (270 J/cm^2) at 850 nm.
LED strength in "mcd" is meaningless. The plastic bulb of LEDs can focus the light to a bright point that has a high mcd rating but as soon as it passes through the skin it's dispersed again as if it were never focused. The important rating is the power per square cm in units of mW/cm^2. A higher mW/cm^2 means less application time is needed. If the manufacturer did not oversize the power supply, the wattage of the power supply should be about 4 times more than the total light energy output of the LED array. The mW/cm^2 is the total light energy in mW divided by the length and width of the array in cm. Your cheek can barely feel the warmth after a few seconds of 30 mW/cm^2 in the 600 to 900 range and 150 mW/cm^2 can make dark skin too hot (> 105 F) after 1 or 2 minutes. Dark skin gets much warmer than light skin from LED devices because the melanin is blocking more of the light, so dark skin requires longer treament time.

From T. Karu, 1996 and 2005
This wide range of wavelengths is specific evidence for the general evolutionary argument that a wide range of wavelengths exactly like the Sun is the best possible exposure. However, there are three ways it might be possible to provide equal or greater benefit than the Sun for hypoxic or injured cells: 1) LEDs can provide injured cells with a larger amount of light in the beneficial range and at times when the sun is not available, 2) we can reduce the heat and thereby provide higher concentrations that reach deeper cells (the Sun is limited to about 1/2 to 1 inch of depth like most LED and laser units), 3) in the future an inexpensive device will be made that is specifically tuned to the CCO set of proteins, having a specific sequence of pulse times of specific wavelengths and pauses, forcing CCO through each step of its pumping action with minimal heat and maximum depth.
A single wavelength may work as good as full spectrum by causing an electrostatic push or pull on neighboring electrons when moving only one electron (into or out of one of the two copper atoms in CCO). The electrostatic push and pull may cascade all the way through the electron transport chain. Complex II activity has been shown to increase even though it does not absorb these wavelengths.
Many different wavelengths have been used, but very few studies have compared different wavelengths. The figure above indicates wavelengths 610-625, 660-690, 750-770, and 815-860 nm are the best wavelengths. Considerations other than how well they activate CCO are: 1) which wavelengths penetrate the best (see section on absorption), 2) which LEDs provide the strongest light output (keep in mind 850 nm has 30% more photons per watt than 630 nm), and 3) possibly 630 nm being usefully absorbed and reflected as (aka "converted to") an 825 nm photon to be used again.
Inexpensive LEDs typically come in 630, 660, 850, and 880 nm with a hard-to-find (expensive) gap between 710 and 830 nm. The peaks of the LEDs and optimum wavelengths are not exact, but spread out about +/- ~10 nm so there is an overlap of available LEDs and the biologically optimum wavelengths. The 630 nm LED can affect the 620nm peak in the chart, and 660 nm LED touches the 680 nm peak, and 850 nm is directly on one peak, but does not cover the nearby peak 820-830 nm as well.

If a "FRACTION" amount of "INCOMING" light remains after a certain "DEPTH" of tissue, then you can determine the light intensity at a deeper or shallower depth of X*DEPTH (where X is a fraction if it is shallower, and larger than 1.0 if it is deeper than DEPTH). The amount of light at X*DEPTH is equal to INCOMING * [FRACTION]^X. For example, if after 1 cm of homogeneous tissue there is 10% of 830 nm light remaining, then at 2 cm there is only 1% light remaining. If a different wavelength, say 850 nm, has 15% light remaining at 1 cm, then at 2 cm it has 2.25% remaining. Notice that 850 was only 50% better at 1 cm, but more than twice as effective at 2 cm, so light penetration considerations are "exponetially important" for deep injuries. This is mathematically equivalent to the more complicated and detailed example below by the following math relation: e^(-k*cm) = [e^(-k)]^cm = (fraction remaining at 1 cm)^cm where k="effective absorption coefficient". My comments above do not assume the width of the array is larger than the depths under consideration, but the standard "absorption coefficients" discussed below do require this condition if they are to be used in the equations. If the source of light is a point source at the skin like a laser instead of an array, then multiply the "effective absorption coefficient" by 2. This is because point sources of any type of ray, not just light, decrease in strength by an r^2 factor as the strength is diluted as it expands into 3D space. Gravity is a famous example of this geometrical surface area effect.
Example: Applying Light to the Skull for the Brain
There is some research looking into light for diminishing ailments such as dementia and mitochondrial disease. For years I told people it was impossible for these healing wavelengths to make it through the skull. But to my surprise, mainly because it seems the skull is thinner than I thought, the math and research says 50% of near infrared (and very likely red) is able to penetrate 3 mm of skull, out of that light that makes it through the skin. For eaxmple, if 20% makes it through a bald head and skin, then 10% appears to make it to the upper layer of the brain. My intuition can't believe it is more than 25% that makes it through the skull by itself, but for this discussion I'll stick with what the math and researchers say. The equation for percent of light transmitted (assuming the applied array is a few times wider then the depth you want to penetrate) is
mW/cm^2 at depth = mW/cm^2 at surface * 2.718^( - effective absorption coeff * depth)
where (effective absorption coeff) = sqrt(3*A*(A+RSC))
where A = absorption coefficient and RSC = reduced scattering coeff = (1-g)*SC where g is anistropy (average cosine of scattering angle) and usually 0.8 or higher.
This can be also used with the charts below. For SKULL BONE A = 0.11 1/cm for red and near-infrared < 900 nm and the RSC = 18 although older papers range from 10 to 40 (reference). The skull is about 0.3 to 0.5 cm thick, giving 2.718^(-sqrt(3*0.11(0.11+18)*0.3 cm) = 48% for 0.3 mm and 30% for 0.5 cm of light makes it through the bone, out of the light that makes it through the hair and skin (so bald, light skin people will get a lot more than people with dark hair and skin skin). This is why it is being studied for dementia, alzheimers, parkinsons, and other mitochondrial dysfunction problems in the brain. Out of interest in this, I put together a helmet of LEDs as shown in the picture below to see if I could notice any effects. After 15 minutes it seemed to put me to sleep. Not a deep or long lasting sleep, but just made me tired-sleepy. It's 1,500 LEDs powered by 160 Watts of 660 nm and 850 nm. Light energy was about 40 Watts, 800 cm^2, 50 mW/cm^2. If 5% of the light made it through, that would have been 2 Watts entering the brain. For comparison, the brain uses about 10 watts.

Don't laugh!
Halogen light bulbs for the brain if you place a gallon zip-lock bag of about 1 quart water on your head then place a $10 500 W halogen flood light from walmart within 1 to 3 inches, then you should get a lot of light energy to your brain. When compared in terms of the energy from LEDs and laser, this should provide about 20 watts in the "mitochondria-active" range (1/3 of the 500 W comes out as light like the sun, and about 1/4 of that light is in the healthy range of 4 wavelengths, and about 1/2 of that is wasted in not being on a specific wavelength like the LEDs). The water is to absorb heat. This assumes the head is bald or shaved. It covers about 200 cm^2 so the intensity should be 20/200 = 100 mW/cm^2 which is twice as intense as my helmet but with maybe 4 times less coverage. Maybe I will do 4 of these 500 W halogen surrounding my head with some water blocking contraption. Skin, etc
The question of what percentage of light is allowed through a particular tissue at a particular wavelength is very important, highly varied, and very complex. For example, there are 5 layers in the epidermis and dermis that have distinctly different absorption and scattering properties that change based on the location and color of the skin. All those variables change again based on the wavelength. An even bigger problem is that usable and reliable data to plug into the equations is non-existent. This is the situation for skin, which is always 1 mm or 1 to 4 mm thick, depending on which source you quote.
I have a excel spreadsheet that tries to follow the methods of Steven L. Jacques and The Science of Phototherapy" but it's pretty much useless. Those sources state anywhere from 5% to 50% of the light in the 600-900 nm range is blocked by the epidermis and 5% to 95% is blocked by the dermis, and the only number for fatty tissue I have results in 99% being blocked by 1 cm.
The graph below shows that wavelengths over 900 nm start to get blocked more and more by water.
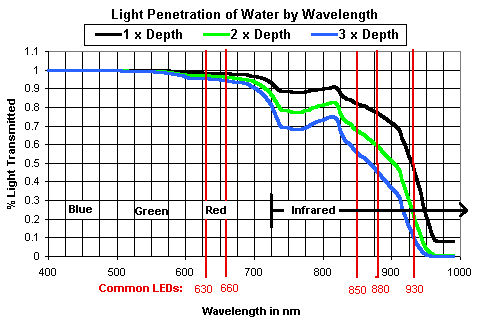
The graph below shows not much light is able to pass through oxygenated blood (HbO2) when the wavelength is less than 600 nm.

Absorption coeff 1/cm = 1E7 * 4*pi* (extinction coeff unitless) / (wavelength nm). Below is the same data, but INVERTED and expanded in our area of interest.

Below is another interesting graph that shows that each mm of melanin in skin is very effective at blocking light, but that layer is very thin (less than 0.005 cm) compared to the small fiber collagen and hemoglobin in the dermis layer (0.1 cm).

For the best info on HbO and Hb in blood see this. and also S Wray. Even if you understand the math, percent light transmission through tissue cannot be calculated unless you can find the %HbO and %Hb (or mM concentrations) in any particular tissue, along with the "baseline" (no blood) absorption and scattering of that tissue. Do that first and please email me the link(s).
Useful Charts:
Water Absorption Factors, 200 nm to 990 nm
Absorption Factor Chart
660 nm verses 850 nm
Wavelengths greater than 800 nm penetrate tissue a little better than wavelengths shorter than 700 (see Light Penetration section). The effect is much larger in dark skin which will benefit more from 850 than from 660. The question is complicated by different wavelengths having stronger or different biological responses. I don't know if one is better than the other, but I currently have a preference for 850 nm over all others. I am in the process of testing other wavelengths to see if I can find anything better than my best 850 device (shown below). 660 nm has a much weaker observed response on CCO, but experiments indicate it works. If 850 nm is better, it might be simply because 850 nm has 23% more photons per mW/cm^2 and CCO is activated on a per-photon basis. (Longer wavelengths have less energy per photon, so equal energy from 850 means more photons). I have not confirmed it, but it appears 850 LEDs are more efficient at emitting light energy than 660 nm and 630 nm, so from a practical viewpoint, circuits of a given style (such as no fan) using 850 nm are simply ABLE to emit more light energy, and LED device businessmen who turn into LED circuit designers, and even professional circuit designers, will not be able to see that the 850 nm spec sheets are saying they can get more light energy out of their circuits than 660 nm designs. The red and infrared spec sheets usually use different ratings (mcd verses mW/cm^2), and it's hard enough adjusting for the "viewing angle" of the LED as it affects the mW/cm^2 and determining if they are talking about 50% level or peak level, not to mention difficulties in conveting with mcd.

660 nm verses 630 nm
When taking penetration and benefits into mind, I do not know if one is better than the other. There are various LEDs in the range of 630 and 660. When I talk about 630 nm, I have 610 to 635 nm in mind, and when I talk about 660 nm, I have 650 to 670 nm in mind. 630 nm red is slightly orange and 660 nm red is a "deeper" red. Since 660 nm is almost infrared, the human eye is not able to see it as well. 630 nm red is used in key rings, traffic lights, and car tail-lights because it's 6 times easier to see than 660 nm (see the photopic response factor - chart ). The eye doesn't suddenly stop sensing light at 700 nm, but it is a gradual decline in sensitivity. You can see the healing and pain relief effect of light therapy by applying a laser pointer or a key ring light to small cuts for 2 minutes or to an arthritic finger joint for 20 minutes.

880 nm verses 850 nm
There are some companies that claim 880 is "the best" frequency, but it appears 880 is absolutely not as good as 850 or 830 nm LEDs. 880 LEDs are putting out frequencies in the range of 870 to 890 and are getting blocked 25% more by water absorption than 850 and the biological response to 880 nm is much less than at 850 nm (see Optimum Wavelengths section).

Measured light output is about 140 mW/cm^2
830 nm verses 850 nm
Judging from the biological response to different wavelengths, it would appear 830 nm is the best of all wavelengths. But 850 nm may be much better for deep tissue as explained below. The 830 nm LED is harder to find, and I don't know if its efficiency is as good as the more common 850. In the end, there may not be any difference between the two.
830 nm is supposed to be better than 850 nm for shallow injuries and possibly better than 850 nm for up to 1/4 inch deep. 850 nm might be better for deeper injuries because more 850 nm reaches deeper tissue. The CCO absorption is the source of all benefit, but 830 nm is being absorbed so well, that it does not make it very deep before all the light energy is absorbed. At some unknown depth, there will be 3 times as many 850 nm photons which overcomes the fact that each individual photon does not work as well as a 830 photon. Mathematically speaking, 830 nm works better by something like 30% but it's exponentially decreasing in strength by something like 10% in the exponential. At some point, the exponential effect on the 10% becomes larger than the 30%. For shallow injuries, 830 nm is definitely working faster, maybe 30% more beneficial, but 850 nm will work just as good if it's applied 30% longer. This means that for the skin or cuts less than 2 mm deep, you would need to apply the 850 nm light 13 minutes instead of 10 minutes for the 830 nm. You save only 3 minutes by using the 830 nm. But for deep injuries more than 1/2 inch, where you might need to apply the 850 nm for an hour, you might need to apply the 830 nm for 2 hours ... a huge difference. A similar discussion is in the 660 nm verses 670 nm section above.
I can definitely feel more heat in my skin from 830 nm devices compared to 850 devices of the same power. This shows more light is being absorbed at a more superficial level. You can feel heat only in the skin, not beneath it, which shows the 830 energy did not make it as deep as 850 nm. At 1/4 inch, 850 nm might be working as well as 830 nm. A 850 nm photon may not be as biologically active as an 830 nm photon at the deeper depths, but at 1/2 inch there may be 2 times more 850 nm photons due to 830 nm exponentially decreasing faster than 850 nm. To see the calculations, review the light penetration section above.
930 nm and above
It appears any wavelength longer than 930 nm will start to have too much of its energy blocked by the water in tissue. See the non-ablative part of the skin section for how 1000-1500 nm can be used to burn the color out of spot and have other beneficial effects.
Blue, Yellow, and Green
See the skin section for information about how blue can help acne (it's really violet, near UV-A) . Blue is about 430 to 485 nm. Green is 510 to 565 nm. Yellow is 570 to 590. None of these penetrate deeper than the skin. See the skin section for how blue can help. There are some companies that claim yellow helps remove wrinkles. I haven't found any research on yellow for the skin that's not conducted by the people who profit from it.

Light Therapy Bed After reading my comments about using halogen lights as a "healing" bed and for the winter blues, someone in Canada in winter 2007-2008 did a great job of implementing the ideas. I had a picture here of my "light bed" and he copied it, doing a better job (see picture below). It uses $5 full-length mirrors, $5 halogen 500 W flood lights, pyrex glass baking pans, and food coloring. The water in the pyrex pans is to block the far-infrared heat. A lot of light energy comes through which warms you up. The food coloring in the water in the pyrex pans blocks visible light energy but still lets the red and infrared through. He actually found the spectrum from the manufacturer of the food coloring which showed the proper wavelengths are allowed through. The food coloring is probably not needed (I wasn't able to tell much difference in the heat, and the Blue/green/yellow wavelengths might be god for the skin). The six 500 W flood lights use a total of 3,000 Watts and would need to be on two different electrical circuits in most U.S. houses without tripping a breaker. It's very calming and can put you to sleep quickly as if you're on the beach....it definitely feels as if you're on the beach. The only bad thing is that there is no U.V. for generating vitamin D which could prevent 50% of breast, colon, and prostate cancers in the U.S. - skin cancer is unimportant by comparison.
2010 update: He emailed: "About 20 minutes on my back then 20 face down.... Kind of makes me really relaxed and sleepy too . . . similar to eating turkey."
2011 update: He reports: "It heals scars and keloids - not immediately, but gradually. Also moles disappear over time, even ones I've had from birth."
Email pictures to me at scott@heelspurs.com if you build a similar set up, and email me after a month and once a year to let me know how it's going so I can post results here.
Halogen Light Therapy Bed (bigger image)

What would it take to do this with LEDs? To cover from the knees to the face, top and sides, about 10,000 LEDs running at 50 mW each with normal spacing of 2 LEDs/cm^2 (12 LEDs/in^2). Power supply would therefore be 500 W. With fans, you can run the LEDs at almost 100 mW each and use half as many (spaced further apart). The 5,000 LED array shown above (with my black New Balance shoe) cost $750 for the LEDs. Someone on alibaba.com is probably already selling this type of healing bed. They should target the 15,000 tanning salons and 50,000 chiropractors in the country. Email me if you find a good one.
Halogen lamps will produce light like the Sun and it can provide more light energy in the healing (tissue penetration) range of wavelengths than regular incandescent and heat lamps. This will be much more energy than LEDs can provide and the energy will be spread out over a larger range of wavelengths (see chart above comparing LEDs and Sun). The halogen is closer to the Sun's natural spectrum. Halogen lamps usually have glass covers that block UV light so that desk lamps do not cause sunburn to hands. The strong blue wavelengths of halogens can be very harmful to the eyes. As with typical LEDs that have about 20% efficiency in converting power input to light output, and as with the wide-spectrum of the sun, halogen lamps also put out about 28% of the energy they use as light energy in the tissue penetration range. So a 75 W Halogen spot-light that concentrates 80% of its light in a 10x10 cm area will produce 75*0.80*0.28/10^2= 0.168 W/cm^2 = 168 mW/cm^2 of light intensity in the tissue penetration range, but the heat from the far-infrared in the skin will be too powerful to keep it there for more than a few seconds. This is about 3 times the best LED array and 5 times the healing range of sunlight. About half of this, 84 mW/cm^2, is near the four specific beneficial wavelengths. To get as much light from a halogen as from the sun, you can compare the heat you feel from a halogen to the heat you would feel from the sun and the healing dosage should be almost as much. Plexiglass can block some of the far-infrared that heats the tissue. Well-designed LEDs will not have the heat problem at all and are not supposed to be harmful to the eyes (I'm still researching it) which are two important reasons they are being used. LEDs are more powerful over a short range of wavelengths which appears to be just as beneficial as having the wattage spread over a wider range of wavelengths as occurs with halogens and the Sun.
Halogen lights contain a lot of blue light and are very dangerous to the eyes.

Comparing halogen, incadescent, heat lamps, and the sun:The Sun, Halogen lamps, incandescent lamps, and infrared heat lamps all emit light based on the black body radiation principle (see this excel spreadsheet if you want to calculate energy in a specified range of a black body spectrum). Halogen lamps have a curve half way between the ones shown for incandescent and the Sun (see this chart). The Sun and halogen lights have about 28% of their energy in the 600 to 900 nm range. Incandescents have 15% to 21% and heat lamps have about 10%. To produce light, halogen, incandescent, and infrared heat lamps heat up a spiral filament of tungsten metal. The filament "incandesces" which means it produces light by black body radiation. A halogen gas can allow the filament to get hotter than regular incandescent bulbs. Heat lamps are the same as incadescent lamps but their long filament is operating at a cooler temperature so that it produces more far-infrared. They operate at approximately the following temperatures: Sun - 5780 K, halogen - 4100 K, incandescent - 2800 to 3200 K, heat lamp - 2400 K. Energy in the far-infrared is easily absorbed by water in the skin, concentrating the light energy in the skin that causes pain from heat sensors.

Simple LED devices for use at home do not work on wrinkles, aging, or scars. Wrinkles are old, fixated collagen, like scars. LEDs repair recent injuries in cells that need more energy. This is the only way they work. There is no reason to believe this will reduce existing scars or wrinkles. Pictures of wrinkles before and after are not comparable because the angle of the lighting and the amount of smiling drastically changes things. I found only one journal article (see below) that indicated simple red and infrared light energy can help.
Low Power Devices for wrinkles and aging:
Spots:
Non-ablative devices are not as serious in terms of risk as ablative (destructive) and they may soon be as good as the older ablative techniques. The non-ablative devices usually use high-energy focused spots of laser light that cannot be duplicated by LED devices sold on the Internet. Wavelengths from 500 to 3000 nm (blue to mid-infrared) have been used, but 1000 to 1500 is being researched the most. These techniques are improving, but are still not as good as ablative. Usually, between >1000 nm and < 1500 nm wavelengths, long or short pulsed, are used to heat the water in the skin to cause heat damage to the cells. Therefore this technology is much different than the 600-900 nm healing wavelengths that the rest of this page is concerned with. Studies have used three to eight treatments typically one month apart. Cryogenic cooling may also be used to minimize harm. At Reliant Technologies, the ablative areas are a about 0.5 mm deep into the skin and twice as thick in diameter as a human hair. "Fractional rejuvenation" or "fractional photothermolysis" is the non-ablative version of the grid pattern used in ablative techniques.
LED light helps only cells that are injured, not dead cells nor scar tissue. Red and infrared LED arrays may help macular degeneration, retinal tear, and laser burns, but very probably not floaters. They could possibly make floaters worse. They are best at treating injuries that have occured within the past few days (the sooner the application, the better). This means about 300 seconds of a typical 25 mW/cm^2 array which is the max officially allowed for infrared before it supposedly heats the lens and cornea. I could not find any information that indicated any normal 5 mm type LED in red could ever hurt the lens or cornea, so you can apply red for longer time periods, but because the pupil response is to become smaller, red is blocked about 5 to 10 times more than infrared, which means it would need to be applied 5 to 10 times longer. My experiments indicated (see pictures below) 5 times more because the area of a 5 mm pupil is 5 times more than a 2.3 mm pupil. I have applied 150 mW/cm^2 850 and 830 nm for 3 minutes several times and did not notice any harm, which is 3 times more than is needed to treat the retina. I believe the ideal array for treating the eye will be 25 mW/cm^2 at 830 nm for 300 seconds while being moved around (definitely not kept still where the retina might be heated too much). 850 nm may work just as well. See the Safety section below on "Retinal Heating" for more information on trying to treat the retina. Especially example 4.



Typically, there are no safety concerns for LEDs unless they are blue or they are really strong or applied directly to the eye.
Heating the Skin
Leaving LED devices on too long and wrap tightly against the skin is probably the most likely cause of harm. Skin temperature should never be more than 41 C (105.8F) to meet FDA regs. Even a weak LED array will cause 2nd degree burns if it is wrapped snuggly with an ace bandage under blankets because the heat is not being allowed to escape. No matter how "cool" a heat-producing device operates, if it's wrapped good enough and long enough, it can get hot. I've found around 0.7 Watts per square inch to be the maximum energy that can be put into a device that touches the skin without a fan or special heat sinking, and even then it will cause 2nd degree burns if there is not an automatic off at 15 minutes and it is wrapped tightly and left in place for over an hour.
Eye Safety
Strong blue and white LED's harm the eyes! Strong green LEDs have 1/15th the risk of blue. Strong and focused Red and yellow LEDs appear safe for at least 5 minutes, as long as they are not the really strong kind like 1 watt and applied directly to the eye.
The ACGIH does not have a safety factor specifically for simple LEDs (as of the last booklet I have which is 1996) because they appear very safe. But it has guidelines to prevent damage to the lens and retina from any light source. The TLV for laser light doesn't apply to non-laser LEDs because lasers are different because they focus the light energy in one spot which is much more likely to cause harm. Blue LEDs may harm the eyes from a photochemical injury called the "blue light hazard" (aka "solar retinitis") that can cause temporary or permanent loss of vision wherever the blue light strikes the retina. This is very dangerous and blue LEDs as key rings should be against the law. Blue is 1,000 times more dangerous than near-infrared of 890 nm (see pdf below, page 5). Red, yellow, and green also have photochemical risks, but only green has the remote possibility of causing harm (if it's high power with a narrow emission angle). Beach and snow always need dark sunglasses for protection against UV and blue damage, and over the long term it helps prevent cataracts from the infrared wavelengths. UV is the most dangerous because it has stronger photons than blue and violet.
Red, yellow, and green are very safe as long as the power is not so high that the retina heats up (this may cause floaters or other less serious "silent" injuries, but I do not have a erference). For yellow, green, and most reds, it will be clear the light is too bright before any harm occurs, unless it is laser light.
Do not assume any of these statements are true when dealing with LEDs. Use this information your own risk.
Lens and Cornea Harmed by Infrared
Cataracts are the more likely source of harm from non-laser, non-blue light, and it occurs from near-infrared and far-infrared (> 770, but < 3,000 nm), but not red. If you work outside or in front of an oven all day for years without eye protection, you are slightly more likely to develop cataracts (in the lens). See long quote below. Glass and thick plastic (safety glasses might be too thin) block far infrared (steel workers) and sunglass for the beach and snow that are not too weak and orange-tinted will probably be OK for the red and near-infrared heat energy. The ACGIH TLV guidelines say infrared eye exposure to prevent injury to lens and cornea should be less than 10 mW/cm^2 if it's greater than 15 minutes. For less than 15 minutes, the TLV guidelines says mW/cm^2 should be < 1800 mW* (seconds)^(-0.75). This equation means that for a typical 25 mW/cm^2 infrared LED device, it's safe to apply up to 300 seconds. These equations overstate the risks of 770 nm to 850 nm from LEDs because the lens and cornea in this range absorb roughly 5 times less energy than longer wavelengths (see links above). Similarly, water and plastic do not hardly block 770 to 850 nm compared to > 850 nm (see charts above). This means 770 to 850 nm make it to the retina seemingly as well as red, which means, like red, they have less energy that can harm the cornea and lens. Red carries even less risk for the cornea and lens. The cornea is the outer covering of the eye that has a bump. It is most sensitve to far infrared such as facing a fire (> 1,300 nm). Closed eyelids protect it. For comparison, staring down at perfectly white beach sand filling your field of vision at noon emits about 25 mW/cm^2 in the near and far-infrared. This is very close to what a typical infrared LED array will emit (including infrared security camera night illumination arrays and infrared flashlights). Devices with fans can acheive 200 mW/cm^2 (like devices I've made for myself: see picture with blue-plastic LEDs way above). I meantion the beach and snow infrared intensity (not counting their UV's and blues) to show that the guidelines indicate they are dangerous even in the infrared, but also to remind you that blue and UV is more dangerous, and to show that the guidelines give more protection than being on the beach for 10 minutes.
This is not an issue for most red and near infrared LEDs, but I need to go into detail because people are applying LEDs directly to the eyes and the information is hard to find, even harder to understand, and this is the only page that shows how to apply the equations to an infrared array (it took me several days to figure it out and type everything below). The retina can be harmed by all visible light and near infrared, but not by far infrared that is blocked by the lens, cornea, and liquid in the eye. Internet references and even books are very poor at explaining the light intensity on the retina, so I'll go into painful detail. There is a discrepency on basics like the eye's focal length. Is the focal length 1.7 cm or 2.2 cm? It's not fixed like most web sites assume because it increases from about 1.7 to 2.2 cm as you focus on objects further away, not counting differences for different size eyes (although different size eyes also have larger pupils so the effect cancels). If you're over 40, about 20 cm is about your shortest focus which gives focal length = 2.2 as lowest value. It's important, because (2.2/1.7)^2 in the equations means 67% higher intensity on the retina if it's 1.7. Someone really near-sighted might have a focal length of 1.4, if I understand it correctly, which would be 2.5 times more light intensity on their retina than others for some of these calculations. Pupil radius increases the light intensity on the retina by a factor of 12 as it changes from dark indoors (0.7 cm) to bright outdoors (0.2 cm), but when I applied 850 nm infrared devices which show a slight red glow (see pictuer above), my retina dilated to only 0.53 cm, which is the max I'll use in the equations.
Equations
All the following assume the light rays are not parallel or converging, but diverging. Steridans measure the "AREA" of a sphere's surface in the same way degrees measure the "LENGTH" of a section of circle. There are 360 degrees in a circle and 4*pi steradians in a sphere. Mathematically:
Steradians = 2*pi*(1-cos(1/2 angle of emission)) = 4*pi*[sin(1/4 angle of emission)]^2 and for small angles = pi*(half angle in radians)^2. Angle of emission in radians as seen at a distance = diameter of source/distance to source.
X = radiance in mW/cm^2/Steradian where the surface areas we'll use for the light source and the receiving object are facing each other and not tilted (so a cosine angle adjustment is not needed).
(1) X = (mW of light source towards receiver) / (cm^2 area of the LED die or light filament as *observed* by the receiver) / (emission angle in steradians towards receiver of the given mW)
X is "radiation intensity" or "spectral radiance" and is very confusing, but very useful because it is the light "radiant flux" (watts) through a surface area that does not change as you get further from the light source, so it is a wonderful constant for a given light source. It is irradiance ( W/m^2 or mW/cm^2) divided by the steridians of the meters^2 at where the watts were measured. The steridians of the meters^2 measurement location depend on how far the measurement location is from the initial source of light.
(2) X = (mW emittedl) / (cm^2 *apparent* size of the light source) / [ 4*pi*(sin(1/4 of emission angle of the mW))^2 ]
angle of emission = 2*arctan(diameter of a distant cm^2 the light passes through / 2 / distance to light source)
(3) X = (mW / cm^2 ) * 1/pi * (distance from source)^2 / (radius of source)^2 assuming the source is small such that sin(radians)~radians and mW/cm^2 is measured at the "distance from source".
(4) (diameter of spot on retina) = (diameter of object) * (inside eye diameter = 2.5 cm) / (distance to object)
(5) 1 / (focal length) = 1 / (inside eye diameter = 2.5) + 1 / (distance from light source to pupil)
Assume (inside eye diameter) = 2.5 cm
eye focal length ~ inside eye diameter ~ 2.2 cm unless it is a young person focusing close, or someone really near-sighted. Not 1.7 cm which is "object focal length".
"Angular subtense" of object being viewed = degrees in field of view = 2*arctan(height/2/distance)
k = fractional amount of light the eye does not block before getting to retina. About 0.90.
(6) mW/cm^2 on retina = X * pi * (pupil radius)^2 / (focal length)^2 * k
(7) mW/cm^2 on retina = mW/cm^2 * (area of pupil) / (area on retina the light is striking) * k
(8) mW/cm^2 on retina = mW/cm^2 / [ 4*(sin(1/4 emission angle))^2 ] * (pupil radius)^2 / (focal length)^2 * k (note: pi in numerator and denominator cancelled)
(9) mW/cm^2 on retina = mW light / (apparent cm^2 area of the LED die or light filament) / (emission angle in steradians) * (pupil radius)^2 / (focal length)^2 * k
(10) mW/cm^2 on retina = mW of laser / area of spot on retina = mW / (pi * (1/2 radian divergence of beam * eye focal length)^2).
This simple last equation works because laser enter in an area that is smaller than the pupil.
Note: given a die size and the watts emitted from the LED, I could not find a way to properly estimate the important X in mW/cm^2/sr it is emitting. For example, say a 0.01 cm^2 die is emitting 300 mW light (i think this is about right for some 1 W LEDs possibly being run a bit hot - the manufacturer maybe should have used a larger die). Right at the surface I can estimate 1/3 of the 300 mW is coming out the front of the die directly, and the steridians for that "half sphere" is about 6, so this gives 100/0.01/6 = 1,700 mW/cm^2/sr, but I don't know how accurate this is, and I don't know how to do it more accurately. It might be off a factor of 2. If the die were a sphere with 0.02 cm^2 surface and emitting 300 mW, then it would be easier: 300/0.02/(4 pi steridians) = 1,200 mW/cm^2/sr. A flat die seems like it should be a little better at directing in a more forward angle, so my 1,700 makes sense. LED lenses seem to not increase mW/cm^2/sr as much as you would think (and maybe not increase it at all) because they increase the apparent size of the die which increases the cm^2 in the denominator even as the mW being directed into a tighter angle is increased.
Example 1:
Take a typical 5 mm type 850 nm infrared LED that outputs a typical 15 mW of light from 50 mW power input. Its plastic case is a little sharper than many, outputting 75% of the light energy into only +/- 10 degrees. What is the mW/cm^2 of the light on the retina at 1 cm away from the eye? At 10 cm? How big is the image created on the retina? How many cones is it hitting?
To answer this, I first need to know how big the LED light source APPEARS after being focused. The die in this LED measures about 0.033 cm on a side which is 0.001 cm^2 area, but this is not what I need (BTW, 100 W/cm^2 die seems to be what a lot of LEDs can be operated at, with 1,000 W/cm^2 peak pulses). The area it APPEARS is a function of how much it has been focused, and I don't know to calculate that from the emission angle. And the LED die sits in a bowl reflector that is reflecting the sides and bottom light from the die. So instead of trying to use guesstimate math, I'll use guesstimate observation and take a picture of this LED in operation (see below, note: total area is 0.055 cm^2, not 0.10, even though I crossed it out). The light shows a lot better in the camera than the dim red that you can see with the naked eye. The radiant intensity is:
Eq (2): X = 15*0.75 mW / 0.055 cm^2 / ( 4*pi*[sin(20/4)]^2 ) = 2145 mW/cm^2/sr
Assume a typical focal length of 2.2 cm (it's not someone under age 35 who is focusing less than 20 cm nor someone strongly near sighted) and a dark room to let more LED light in so pupil radius = 0.6/2 cm.
Eq (6): mW/cm^2 on retina = 2145 * pi * (0.3)^2 / (2.2)^2 * 0.90 = 110 mW/cm^2 at all distances, which provides a nice 6 J/cm^2 treatment in 55 seconds.
Width on retina of the image at 1 cm and 10 cm:
eq (4): width = 0.16 cm * 2.5 / 1 = 0.4 cm
eq (4): width = 0.16 cm * 2.5 / 10 = 0.04 cm
A length of 0.04 cm * 3,800 cones/cm = 150 cones
Notice image size on retina is the only thing that depends on distance. So the image gets smaller as the LED is further away, but the intensity of light per cm^2 does NOT. So if the intensity were dangerous to individual rods and cones like blue or UV light, then it does not matter how far away you get, cells would still be injured. This is long as the diameter of the image on the retina is larger than 1 rod or cone (a 0.2 cm arch weld from eq (4) covers 1 cone at 66 feet but I have not verified this).

Example 2:This is a lengthy and wide-ranging "example" is more of a discussion and illuminatino of complicating factors that ends with an example. My infrared LED emits from the front surface the 5 mW per 0.033x0.033 cm die. 5 mm LEDs can often be pulsed with 10 times higher amps with a 10% duty cycle (others like SMD and super bright can pulse only 60% higher), but the rods and cones are not likely to know the difference with pulsing because they require heat build-up to "melt" just like the semiconductor, so it balances out in terms of safety (and how strong the light appears). It appears 1 W LEDs have dies about 0.1 cm wide and at 30% efficiency, they might be emitting 300mW/0.1^2 = 30,000 mW/(die cm)^2. Coming directly out the front surface might be half of this, 15,000 mW/cm^2 die, which is 3 times higher than my infrared LED. This makes sense: the 5 mm LEDs can't be run as intense continuously per die area, but can be pulsed higher. This implies the 5 mm LEDs can't dissipate heat as fast and that the peak pulse of amps depends on the die area. So it appears the 50 mW 5 mm LED and the 1,000 mW white LED can reach similar max temperatures and similar max peak watts per cm^2 of die area. This has importance in trying to understand generalizations about the safety of LEDs in terms of thermal effects on the retina (I will not discuss blue hazard because it is more clearly dangerous and things are complicated enough trying to determine red and infrared safety). Getting back to this "example", let's assume no LED plastic cover is converging the light on a spot smaller than the die area itself but only directing the light forward that would normally get lost to the sides. So at max it is a perfect laser who's beam is not diverging even a little like normal lasers. LED focusing can't be nearly as good as lasers and even lasers can't be exactly parallel rays, but I want to look at most intense case for LED dies. Let's say the die is infinitely wide and tall and there's no focusing (rather, instead of focusing to make it equal to the worst case of non-converging focusing and easy to calculate). This is a "worst case" for safety by trying to make it maximum intensity. Focusing can't be stronger than this unless the focusing is converging the rays onto a point rather than simply directing the light in a more "forward" direction. This does not increase the intensity of the light per cm^2 PER DIE AREA as it appears on the retina because that type of focusing (non-converging) makes the die APPEAR bigger as in example 1 (as the mW increases from focusing, the apparent die aera increases, so there is no net radiant intensity increase: mW/cm^2 of die area I think might be a constant). So an LED casing is more like a microscope which needs more light on the object to see it because the objective lens is small compared to your pupil but not like a telescope which has really large optics to focus DOWN the light into your pupil. Getting back to this example's theoretical infinitely wide and tall die, there is a rule that says for a flat plane emitting any type of rays per cm^2 like light, sound, or gravity the strength will not diminish over distance. This is because as it tries to get weaker with distance, contributions from the sides increase to balance it out. So the mW/cm^2 of the die will be the mW/cm^2 that your pupil sees. Let's guess that no commerical LED die constantly emits more than 30,000 mW/cm^2 per die area, and so the pupil will see 30,000 mW/cm^2 (no steridians in denominator because I tricked it to go away with an infinte die) from this huge die. This is 300 times the strength of the Sun but it covers the entire the font field of vision rather than a single spot like the Sun. The Sun is 0.53 degrees instead of 180 degrees which is 100,000 times less surface area (steridians) of the emission source. So, the die is 300 times stronger mW/cm^2, but coming from 100,000 times more surface area, giving 300/100,000 = 0.003 times less "radiance" (radiant intensity mW/cm^2/sr) that is important in terms of intensity as a spot on the retina. Said another way, this very large LED's 30,000 mW/cm^2 hits the pupil, and it SPREADS OUT across the much larger retina area. The pupil's hole is at most pi*(0.7/2)^2 = 0.38 cm^2 (infrared LEDs would allow this) letting light through and the retina is about 13 cm^2, so the average intensity should be roughly based on this ratio of areas: 30,000 * 0.38 / 13 = 900 mW/cm^2 on the retina. More precisely, using the focal length and equation (8), I get 341 mW/cm^2 so the method of simply dividing by the area of the pupil by area of retina is a 2.5x over-estimate. Eq (8) for the Sun's 100 mW/cm^2 gives 106,000 mW/cm^2 spot on the retina. Dividing 341/106,000 = 0.003 less from the LED as predicted above. But using a better number for the pupil radius as in the next example gives a much lower 8,700 mW/cm^2. A small change in pupil radius can have a large effect because it is a squared factor. 8,700 / 341 = 25, meaning the Sun is roughly 25 times worse on a spot of retina than the most massive and dangerous red or infrared LED I can imagine. Since the small spot from the Sun dissipates heat better, the safety difference is actually much less than 25. Once the correction for "retina heat dissipation" is made, such a large LED die is more dangerous than the Sun, and for the entire retina, not just a spot.
Example 3:
Sun, eye focused at a distance (focal length=2.2 cm), bright outside (pupil radius = 0.2/2). Sun insolation is 100 mW/cm^2 and is 0.53 degrees in the sky:
Eq (8) mW/cm^2 on retina = 100 mW/cm^2 / [ 4*(sin(0.53/4))^2 ] * (.1)^2 / (2.2)^2 * 0.9 8,700 mW/cm^2
This heat energy is the upper bound of what is safe for 1 second exposure. The real danger from the Sun is the blue and UV which are not part of the considerations in this section. We are designed to cope with the Sun in our peripheral vision for most of the day. This gives an idea of how safe red and infrared LEDs.
Example 4:
Apply a 25 mW/cm^2 from a typical 850 nm infrared ARRAY to the eye in a dark room. In order for this calculation to be more accurate, the array needs to be far enough away that the LEDs appear similar in strength which indicates their light beams are overlapping. If the array is close and the emission angle is small, then only 1 LED will appear bright for a very small section of retina and you would just use example 1 for that 1 LED. For an array, you are not getting a nice and even mW/cm^2, but you get an array of spots on the retina where each spot corresponds to example 1 (75 mw/cm^2 per spot). So to get an even treatment, the array should be moved in tight little circles. The tighter-angle LEDs will have to be further away to appear the same strength, which means the array has to be wider to cover a large area. The following is for 25 mW/cm^2 850 nm array, at +/- 15, +/- 10, and +/-5 degrees emission angles, a dark room (0.6 pupil), and not trying to focus at a close distance ( 2.2 cm focal point):
Eq (8) mW/cm^2 on retina = 25 / [4 (sin(5*2/4))^2 ] * (0.53/2)^2 / 2.2^2 * 0.9 = 43 mW/cm^2
Eq (8) mW/cm^2 on retina = 25 / [4 (sin(10*2/4))^2 ] * (0.53/2)^2 / 2.2^2 * 0.9 = 11 mW/cm^2
Eq (8) mW/cm^2 on retina = 25 / [4 (sin(15*2/4))^2 ] * (0.53/2)^2 / 2.2^2 * 0.9 = 4.5 mW/cm^2
These numbers are only if the array is being moved around in the field of vision. If stationary, then use example 1 for each spot the array creates on the retina. The 11 mW/cm^2 for +/- 10 degrees is 10 times less than for a single LED kept still as shown in example 1. This implies the "no-light" area where there is not LED light from the circuit board as seen by the eye is 10 times the area of the light seen coming from the individual LEDs. In example 1 I observed the LED light per LED covering 0.055 cm^2. I use these LEDs to produce 25 mW/cm^2 arrays and I space them 2 LEDs/cm^2. So the light is coming from 2 LEDs (0.11 cm^2 of light) per 1.0 cm^2 of circuit board space, a factor of 10 difference, right in line with these calculations.
For a red LED, the pupil will be 0.23 cm instead of 0.53 cm giving: 7.4, 1.9, and 0.8 mW/cm^2 which is very small.
If I were treating my retina I would use an infrared array with +/- 5 or +/- 10 degrees LEDs. Treatment time is to get about 6 J/cm^2. For example, at 25 mW/cm^2 with +/- 10 degree LEDs, retina gets 11 mW/cm^2 which would be 6/0.011 = 545 seconds = 9 minutes as a max, maybe 3 minutes as a minimum that may be enough to get good benefit. More than 10 minutes may start reducing the benefits. According to the TLV safety guidelines below, more than 5 minutes is not safe for the lens and cornea at 25 mW/cm^2 at 850 nm, but I believe they are being too strict for this wavelength as detailed above. It will be hard to know how many mW/cm^2 an array is supplying unless an experienced person looks at the operating array, or if the manufacturer actually knows his specs rather than guessing from data sheets. 25 mW/cm^2 will be what a good security camera illuminator array from ebay will provide, given that they use 5 mm LEDs spaced about 2 per cm^2 and you can easily see the red glow from the 850 nm LEDs in a lighted room. There is a section above that shows how to measure it if the measurement is done carefully and correctly. The retina does not block much infrared light according to one source, so the back of the retina is being treated too. Clearly retinal tears and laser burns within the past day or two need to be getting infrared treatments before the cells die. Anyone else copying what I would do for myself assumes full responsibility for the results.
Retinal Safety Calculations
The ACGIH TLV safe dose for for the retina for green, yellow, red, and near infrared is anything that causes one of the following to be less than 1:
for 1 us to 10 seconds: 1/5000 * X * (width of source) / (distance to source) * seconds^0.25
The above is for 500 nm to 700 nm thermal only. I won't discuss blue light hazard which is a different topic. for 700 nm to 1050 nm multiply by 10^[(700-nm)/500]
for > 10 seconds: 1/600 * X * (width of source) / (distance to source)
this second one is based on a 7 mm pupil and a detector field of view of 11 mrad (i don't know what that means). At 10 seconds this seconds equation comes out about 8 times more dangerous than the first. There is another equation for cornea and leans safety, but it seems to be 10 or 100 times "safer" (less likely to affect cornea and lens) at less than 100 seconds, and many times more dangerous at 1000 seconds or greater (see previous comments). The "width/distance" is a factor that adjusts for smaller spots on the retina which are less dangerous because the heat can spread better to the sides of the retina, as long as the spot is less than 1.7 mm. If the spot is larger, this ratio is no longer has an effect. 1.7 mm spot is supposed to be 0.1 radians (source of light has a diameter 1/10th the distance to the eye), so that for ratios larger than 0.1, make the ratio a constant of 0.1 rather than further penalizing the source. However, I did not see where the ACGIH says this and even gives an example using 0.5 radians. So maybe the ratio is not meant to show small spots are safer, but to show larger spots are more dangerous.
The danger to the retina could be thermal burns that do not heal (blindness in spots) or maybe more floaters obscurring a little bit of vision from the internal fluid pulling away from retina a little more.
Example 5: (most dangerous red/infrared LED example)
For 10 seconds apply 1 Watt 660 nm or 630 nm LED outputing 75% of its 300 mW within +/- 20 degrees at 1 cm in front of pupil . Assume die area is 0.1x 0.1 = 0.01 cm^2 but that the focusing lens makes the die appear 5 times wider.
1/5,000 * 300 mW*0.75 / (4*pi (sin(20*2/4))^2) * 0.1*5 / 1 * 10^0.25 = 0.066 (supposedly safe by 1st calculation)
1/600 * 300 mW*0.75 / (4*pi (sin(20*2/4))^2) * 0.1 / 1 = 0.31 (supposedly safe, but not. See below)
If the angle of emission is +/-10 degrees, then multiply these numbers by a factor of 4, so the bottom is unsafe. Actually, since there is focusing into a small angle, the LED die will appear larger than it's actual 0.1 cm width, so these numbers are probably not safe (the 0.1 number should be larger, maybe 5 times larger).
Example 6: Typical 850 nm 5 mm LED safety.
Using data from example 1, hold a 850 nm LED 1 cm from pupil for MORE than 10 seconds: 1/600 * 2145 mW/cm^2/sr * sqrt(0.055) /1 = 0.82 This gives < 1 therefore supposedly safe for any length of time. Looking at the LED this "apparent die size after focusing" is not "contiguous" (there are gaps between the light) so that the retina may be able to dissipate the heat better than I'm implying, so it should be safer than this by a factor of about 3. Manufacturers may desire "contiguous" light from the focusing lens but this shows that is not desirable from a safety standpoint. An array of these will not be more dangerous than the individual LEDs, but simply affecting more spots, if it does have an effect. However, 5 mm LEDs can be run at 2 or 3 times than their ratings for 10 seconds without burning up. If they are kept cool with a fan they will still be efficient in turning the energy into light. So it is possible to run a 5 mm red or infrared LED in a way that it is not safe to look at it within a few cm of the eye. My guess is that it would be difficult for them to be harmful at more than 10 cm from the eye. LED Array: if the array is moved around in the field of vision, then the 2145 mW/cm^2/sr is effectively 10 times smaller as described in an example above, so arrays being moved around to treat the retina should be safe.
Example 7: Sun safety.
1 second staring at Sun. Sun insolation is 100 mW/cm^2 and is 0.53 degrees in the sky.
X = 100 * 1/pi * (distance to sun)^2 / (sun radius)^2 = 1,460,000 mW/cm^2/sr
Safety calculation: 1/5000 * X * 1.4E6/1.5E8 * 1^0.25 = 2.6 which is > 1.0 so it's risky even for a second if this is going to occur often in the work environment, not counting the UV and the much more dangerous blue light hazard.
Example 8:
Sun for > 10 seconds in one spot on eye: 1/600 * X * 1.4E6 / 1.5E8 = 23, very dangerours.
Lasers
are covered on other web pages, but here's the equation and calculation for comparison:
mW/cm^2 on retina = mW of laser / area of laser spot on retina = mW / (pi * (1/2 radian divergence of beam * eye focal length)^2.
Example 9: standard class IIIA, for presentations, 4 mW laser pointer, 0.001 rad divergence (I tested mine at 30 feet to confirm this):
mW/cm^2 on retina = 4 mW / (3.14*(0.0005*2.2)^2) = 1,760,000 mW/cm^2
This is 200 times more than the Sun. The only saving grace is that it is usually moving fast across the eye in a very small spot so that the tissue absorbs the 4mW heat energy. The small spot getting all the energy is the problem in the first place, but my point is that if it were as wide as the Sun (8 times wider), then it would not be 200 times more dangerous, but 8 times smaller is 200/8 = 25 times more dangerous, except the Sun has blue and UV which is the usual source of harm if you don't count life gaurds on white sand beaches who don't use sunglasses.
When the light beam is smaller than the pupil, the pupil radius is not in the equation.


Designers trying to select LEDs or arrays will have trouble comparing LED brightness from different manufacturers. The plastic encasings can focus the light and make mcd ratings much higher, but the amount of light coming out is the same. A 100 mcd LED at +/- 10 degrees (20 degrees angle of output) has the same total amount of light output as a 2,000 mcd LED at +/- 5 degrees (10 degrees). The equation is: Milliwatt output of an LED = mcd / (683 x P) x 2 x pi x (1-cos(1/2 Angle of output)). Companies are not exactly consistent in how they measure mcd (millicandela) and the angle output. Be careful in determining if they are stating 1/2 angle or full angle. P is the "photopic response factor" ( graph ) that depends on the wavelength. mcd and P are only meaningful for visible wavelengths (not infrared). P=1 for 555 nm and P=0.061 for 660 nm. For infrared, the measurement has to be mW/SR where SR=steradians. SR units are the percentage of a sphere's surface area, but divide SR by 4π (12.566) to get the percentage. SR is to a sphere as radians are to a circle. To convert from angle of output to steradians, use SR = 2 x pi x (1-cos(1/2 Angle of output)). Replace mcd/(683 x P) with mW/SR for infrared LEDs. In practice all this is not very useful. You just have to buy the LEDs and compare them. All 850 nm LED lamps I've tested had the exact same efficiency. As a rough estimate, the light output energy of an LED is 30% of the input energy. Strong LEDs use 50 to 100 mA continuously. But 20 mA red LEDs can put out enough light and are very common. A good and strong 850 nm LED will use 50 mA continuously, but the device will get too hot if you pack the LEDs closely (22 LEDs per square inch for 5 mm packages) and run them anywhere near their max. 0.8 watts per square inch is the maximum energy you can apply to any device that touches skin unless a fan or heat sink is used in order to the skin temperature below 105 F (FDA guideline). Kind of like a high fever on the skin, except the blood is able to take away the heat. So at a typical spacing of 12 LEDs per in^2 (2 LED per cm^2) you can apply 66 mW per LED. That's 45 mA at 1.55 V for the common 850 nm lamp and 35 mA at 1.9 V for a good 660 nm. LED spectrums can be generated with this spreadsheet.
Despite all the above, in directly measuring LED strength as described below, I measure only half the intensity reported by the datasheets. Datasheets report very roughly 1/3 of the energy input coming out as light output. I measure only half as much, about 18%. An expert on this tells me you can expect 15% to maybe 30% light ouput from LEDs used in light therapy.
You can measure the light intensity of anything in mW/cm^2 by using a styrofoam cup, cocoa powder, coffee or another water-blackening agent, and a home digital thermometer (accurate to 0.1 or 0.2 degrees C), based on the heat capacity of water. The equation is: W/cm^2 = 2cm x C x 4.18 / seconds where 2cm is the depth of water with dark cocoa powder to make it black water, C is increase in the water's temp, 4.18 is converting from calories to Joules, and seconds is the time the light was applied (200 seconds works best for high power device, up to 600 seconds for typical low power). The styrofoam cup needs to be cut off at 3 cm and LEDs can't be too close because air currents cause direct heating from the LEDs. For LED devices too small to cover the surface of the water, apply the light for longer amount of time and multiply the results by the water surface area divided by the surface area of the LED array. Do not take temp measurements in the sun or while the LED device is being applied because the metal absorbs the light and heats up. Water temp must be close to room temperature. For a simple red or infrared LED array running at about 30 mA per LED I get about 30 mW/cm^2 from 2.1 C rise after 10 minutes. My results are typically half of what LED manufacturer's data sheets say. I know the data sheets are wrong because their data is not usually self-consistent and my measurements of sun intensity are very accurate to the known intensity (100 mW/cm^2 when sun is > 80 degrees in the sky). The sky should be blocked from giviing light to the measurement cup bacuase reflections from the sky can provide 5 to 15% more light. To calculate sun intensity at any time at any location on a sunny day, use this spreadsheet.

"But if the rats were treated with LED light with a wavelength of 670 nm for 105 seconds at 5, 25 and 50 hours after being dosed with methanol, they recovered 95 per cent of their sight. Remarkably, the retinas of these rats looked indistinguishable from those of normal rats. 'There was some tissue regeneration, and neurons, axons and dendrites may also be reconnecting,' says Whelan." "We believe that the use of NASA Light-Emitting Diodes (LED) for light therapy will greatly enhance the natural wound healing process, and more quickly return the soldiers to a pre-injury/ illness level of activity. The use of LED in combat with self-healing patches in future may enable the soldiers even after they are wounded to persist in combat better and longer." http://www.asc2002.com/Abstracts_only/d/DA-06.pdf
"LED produced improvement of greater than 40% in musculoskeletal training injuries in Navy SEAL team members, and decreased wound healing time in crew members aboard a U.S. Naval submarine. LED produced a 47% reduction in pain of children suffering from oral mucositis. CONCLUSION: We believe that the use of NASA LED for light therapy alone, and in conjunction with hyperbaric oxygen, will greatly enhance the natural wound healing process, and more quickly return the patient to a preinjury/illness level of activity. " "ATS treatments improve sensation in the feet of subjects with DPN, improve balance, and reduce pain."
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&dopt=Abstract&list_uids=11776448
"This technology may be the answer for problem wounds that are slow to heal....diabetic skin ulcers and other wounds in mice healed much faster when exposed to the special LEDs in the lab. Laboratory research has shown that the LEDs also grow human muscle and skin cells up to five times faster than normal...."
"Light close to and in the near-infrared range has documented benefits for promoting wound healing in human and animals. "
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&dopt=Abstract&list_uids=11568632
"ATS treatments improve sensation in the feet of subjects with diabetic peripheral neuropathy, improve balance, and reduce pain."
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&list_uids=14693984
"Near-infrared irradiation potentially enhances the wound healing process, presumably by its biostimulatory effects."
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&list_uids=11722751
" It was found that laser exposure resulted in more pronounced restoration of functional state of nervous fibers than conventional therapy. Application of laser irradiation of low intensiveness was effective while in combined therapy of distal diabetic polyneuropathy as well as monotherapy."
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&list_uids=9677693
"exposure of volunteers to visible and infrared polarized (VIP) light leads to a fast increase in the growth promoting (GP) activity of the entire circulating blood for human KCs in vitro, which is a consequence of the transcutaneous photomodification of blood and its effect on the rest of the circulating blood volume."
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&list_uids=14743286
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&list_uids=14521091
"The method of monochromatic near infrared stimulation can be used for selective stimulation of several regions of the external auditory canal,.."
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&list_uids=14999583
LED and LLL irradiation resulted in an increased fibroblast proliferation in vitro. This study therefore postulates possible stimulatory effects on wound healing in vivo at the applied dosimetric parameters.
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&list_uids=12928819
Wound healing was significantly more rapid with than without FIR. Skin blood flow and skin temperature did not change significantly before or during far-infrared irradiation.
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&list_uids=12773705
Although more studies are needed, LED therapy appears useful in the prevention of OM in pediatric BMT patients.
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi
News articles on the NASA Study:
http://garm.dyndns.org/whelan_lab/01/html/%20/whelan.html
http://www1.msfc.nasa.gov/NEWSROOM/news/releases/2000/00-336.html
http://healthlink.mcw.edu/article/975450257.html
http://www.hypography.com/article.cfm?id=29173
http://www.viahealth.org/via_news/news2002/april/woundstudy.htm
http://www.engr.wisc.edu/industry/atwork/vol5/WCSAR.html
http://www.scienceblog.com/community/older/archives/D/archnas202.html
A wound-healing device was placed on the USS Salt Lake City submarine, and doctors reported 50 percent faster healing of crewmember's lacerations when exposed to the LED light. Injuries treated with the LEDs healed in seven days, while untreated injuries took 14 days.
second daily infrared (JR) laser (820 nm, 25mW) and visible red laser (670 nm, 10 mW) at 1 J/cm2 and 5 J/cm2 on chronic pain. ...five treatment sessions over a two-week period. ...significant reductions in pain over the duration of the study with those groups which received infrared (820nm) laser a 1 J/cm2 and 5 J/cm2
904 nm three times weekly for 2 weeks, ......tendonitis of the shoulder
3.5-inch by 4.5-inch (89-millimeter by 114-millimeter), portable flat array of LEDs, arranged in rows on the top of a small box. ......places the box of LEDs on the outside of the patient's cheek about one minute each day. The red light penetrates to the inside of the mouth, where it seems to promote wound healing and prevent further sores in the patient's mouth.
All 176 patients received six treatments during a period of 3-4 weeks. ..GAAs laser therapy for tendinitis and myofascial pain
A 40 year-old woman presented at the Abe Orthopedic Clinic with a 2-year history of lower back pain and pain in the left hip and leg diagnosed as a ruptured disc between the 5th lumbar/1st sacral vertebrae. .....The gallium aluminum arsenide (GaAlAs) diode laser (830 nm, 60 mW) was used in outpatient therapy, and after 7 months, the patient's condition had dramatically improved, demonstrated by motility exercises. This improvement was confirmed by further MRI scans, which showed clearly the normal condition of the previously herniated L5/SI disc.
Influence of low-level (810nm, GaAlAs semiconductor) laser on bone and cartilage during joint immobilization was examined with rats' knee model. .......The hind limbs of 42 young Wistar rats were operated on in order to immobilize the knee joint. One week after operation they were assigned to three groups: irradiance 3.9W/cm2, 5.8W/cm2, and sham treatment. After 6 times of treatment for another 2 weeks both hind legs were
myofascial pain in the cervical region. The patients were submitted to 12 sessions on alternate days to a total energy dose of 5 J each.
RA:From July 1988 to June 1990, 170 patients with a total of 411 affected joints were treated using a GaAlAs diode laser system (830 nm, 60 Mw C/W). Patients mean age was 61 years
890 nanometer (nm)....Venous ulcers, diabetic ulcers, and post-amputation wounds....It recently has been demonstrated that application of this particular MIRE device to the skin for 30 minutes increases plasma NO in nondiabetic subject volunteers, as measured with a Sievers Instrument, Model 280, Nitric Oxide Detector
© 2004-2012 heelspurs.com LLC
Author: Scott Roberts
scott@heelspurs.co
Introduction
This article is about red and near-infrared light therapy for healing recent injuries and a few other possible things like fibromyalgia pain, dementia, retinal injuries, and wrinkles. This is closely related to (if not identical in results) to LLLT (low level laser therapy) but it usually uses LEDs instead of weak lasers. For example, you can shine a red laser pointer on a cut for a minute or two to see the pain go away. This article does not discuss SAD, psoriasis, acne, and jaundice which are helped by white or blue light.This article has been around for years and I'm constantly updating it. Here are 3 errors in previous editions that are mostly corrected in this edition:
- Proper pulsing may be extremely useful. I have a product I'm about to sell that uses a particular type of pulsing.
- Red and near-infrared light *can* make it through 3 mm of skull bone.
- Light therapy *may* be useful for wrinkles, photoaging, and baldness

LED light arrays are a means to provide these wavelengths. Companies may claim lasers and pulse rates are important, but the only things are the wavelength and total amount of light energy applied. For example, 880 nm is a bad choice. Bright noon-time summer Sun only has half as much light energy as LED devices in the optimum wavelengths, but it covers the entire body (which is good for fibromyalgia). The advantages of LEDs over sunlight are: 1) LEDs can be applied at any time, 2) LEDs require only one hour instead of two hours for injuries beneath the skin, 3) LEDs don't cause sunburn.
Halogen lights emit a spectrum of light that is very similar to sunlight (see this chart or this). Like bright sun, halogen provides an inexpensive source of "healing light energy" in the 600 to 900 nm wavelengths (see Halogen Lights section below), but the energy is not concentrated at the best wavelengths as in LEDs. My interest in light therapy increased a great deal when a halogen treatment returned my black-and-blue broken small toe to almost a normal color in 5 minutes. Pain level went from 8 to 2. I repeated the treatment 6 hours later when the toe turned blue and painful again and received the same benefits.
Heat lamps have long been used to reduce pain. It was believed the heat provided a benefit, but now we know the near-infrared portion of the spectrum of heat lamps provides more benefit than the heat of the far-infrared.
Conditions Helped
Conditions that are probably helped- osteoarthritis (full-body Sun exposure is best, without sunscreen)
- sports injuries such as knee, ankle, shoulder, etc
- burns, scrapes, and cuts. Skin might be already optimized for healing rate, but strong devices can immediately eliminate moderate pain. Burns need to be covered, but between changes it might be very beneficial, or use saran wrap instead of gauze. Possibly 3 to 6 treatments per day is not too much, depsite some research claiming once per day.
- ulcers (on skin, not in stomach)
- macular degeneration (see safety)
- laser burns to the retina (see safety)
- fibromyalgia pains (full-body Sun exposure is best, without sunscreen)
- preventing bruising and inflammation if it's fresh injury
- tendinitis (My 2 tendinitis problems were helped a lot more by stretching and massage)
- back pains (hit or miss depending on depth)
- bunion pain
- diabetic neuropathy
- restless leg syndrome1 2
- myofascial pain
- fractures (possibly)
- inflammation (iffy if it is chronic, but 850 nm is supposed to be the best)
- minimize recent nerve injury
- bursitis
- dementia, mithochondrial disease, Alzheimer's, Parkinson's
- Cancer. Light therapy increases the cell's ability to use food energy. Cancer cells might use this, or the cells surrounding the cancer may need it to stop the cancer. Methylene blue and other photo-active chemicals can concentrate in tumors and then applying 660 red light can activate the chemicals, causing them to turn toxic to the cancer.
- Compressed nerves
- wrinkles, aging, acne, spots (see skin section)
- bone union (it might help, but it the bone is not close to begin with...)
- retinal tear, floaters (see safety LEDs for long periods may cause floaters)
- existing bruises
- rosacea, psoriasis, eczema, dermatitis, poison ivy
- headache
- muscle ache from working out (my experience)
- infection
- scars
- bunion reduction
- reverse osteoarthritis bone deformation
- any injury too deep. I'm especially skeptical of anything more than 1.5 inches deep. How much red light can you see get through an inch of your palm (which is 2 layers of skin). None, not even with the strongest devices, and near infrared is not any better.

How useful is light therapy? I view red and infrared light as equally beneficial regardless of the source (sun, halogen, LED, or laser) as long as the intensity and area of coverage are equal. I think 830 nm is best, but maybe 660 nm is better, and in either case, you can just make the less beneficial wavelength have a stronger light source. There is no theory that indicates the effects are different. They kick-start injured cells into making more ATP. I view red/near-infrared light therapy as beneficial overall as applying ice to injuries, keeping in mind that people greatly under-utilize ice. More important than ice and light for joint injuries is a lot of stretching, movement, and careful strengthening. I use light mostly immediately after an injury, right before applying ice for 5 minutes, and then repeat once every 6 hours for a day or two. Immediately after injuries, ice is more important.
FDA allows advertising red and infrared for minor pains and mild arthritis. Red has been used to help halt dry macular degeneration which may have FDA approval. The following have FDA approval for specific devices (these are just those I know. I have not done a search): infrared 880 nm for diabetic peripheral neuropathy, 660 nm red for mouth ulcers in children on a type of chemo, "Titan" intense infrared device for wrinkles in a clinical setting, very intense (harmful) infrared devices for spots, and blue or blue/red for acne. There have been excellent results reported for tendonitis, shoulders, knees, small joints, and fibromyalgia. For most soft-tissue injuries beneath the skin, the pain goes from an 8 to a 2 (on a scale of 10) after an hour or two of treatment with good home-use LED devices. For exposed injuries like burns and retina injuries, only 1 to 10 minutes of LED light is used, depending on the device. Applying LED light for too long cancels the benefits, but the time of application is hard to determine. Too little light and there is little benefit, and too much light and there is no benefit. For injuries where the pain can be felt, I apply it only long enough to notice the maximum pain relief and no longer. The pain relief can be amazing in burns, cuts, and other wounds even if wound healing is not faster. The increase in the speed of healing can be directly measured in the injured retinas of rabbit. Stubbed toes can go from being purple-black to pink in one treatment. Serious injuries seem to benefit from 3 to 6 treatments/day (as the pain returns) instead of one treatment/day. Strangely, tendon and muscle soreness from working-out seems to not receive any pain relief, but chronic tendinitis seems to benefit greatly. From my experience in trying to help friends and family, it is beneficial only about 30% of the time in back pain. Companies have made various strange claims that I do not believe: yellow for wrinkles, green for cancer, and blue for wrinkles. Recent serious injuries benefit from several treatments per day.
In hindsight, we can say "people have always known Sunlight is good for you". It seems intuitively clear to most people that Sunlight helps sick people and enables people to be more active. We know why from a chemical and biological viewpoint. Injured cells need the extra ATP to repair themselves. Healthy cells may generate extra ATP from the red and near infrared of sunlight to enable more activity in the daytime. If the ATP is not used (as occurs when resting in bright sunlight) it causes an increase in available glucose for which causes a slight "glucose high" that causes relaxation and sleepiness we all feel after 30 minutes in the sun. BTW, we know UV creates vitamin D that prevents colon, prostate, and breast cancer, greatly improves the immune system, bone strength, and reduces the incidence of osteoarthritis, having the potential to save 50,000 lives a year if people would get more Sun and wear less sunscreen. By comparison, skin cancer causes less than 10,000 deaths in the U.S. each year, only some of which are caused by too much Sun.
How does it work?
The wavelengths from 600 to 900 nm pass through blood and water in tissue more easily than other wavelengths. About 35% of the energy in this range is absorbed by a specific "proton pump" (cytochrome c oxidase, CCO, "complex IV") in mitochondria. The light at 4 specific wavelengths "kick-start" the CCO pump into producing more cellular energy, ATP. The CCO pump is very similar in all animals because the key proteins were inherited from light-assisted bacteria that were part of the first mitochondria. The absorption spectrum of blood suddenly drops off to allow these wavelengths to pass through which indicates the evolution of hemoglobin may have been influenced by cells benefiting from these wavelengths. The immediate increase in respiration that Sun causes by this mechanism may help animals increase their activity during the day, in addition to the heat provided by the sun that promotes the release of oxygen (myoglobin also absorbs these wavelengths). These wavelengths of the Sun can provide the optimum 4 J/cm^2 at a depth of 1 inch (using 1% transmission) after 1 to 3 hours of exposure in bright Sun, reaching all skin and a large percentage of muscle tissue in historically-thin humans with minimal clothing.Evolution Theory Support: There are 5 indications that the benefit of red and near-infrared light is not an accident, but a highly "intelligent" and natural result of evolution. The indications are: 1) The proton pump is the last in a series of 3 pumps which places it in possibly the best location to pull the food conversion process along by "pushing" the final electrons through the chain. This creates electrostatic pull on the electrons further back in the chain. 2) The pump absorbs primarily the red and near-infrared light and the remaining sunlight wavelengths are blocked by water and blood. 3) The pump is the primary absorber of these wavelengths in the body, very roughly about 35%. 4) Oxygenated hemoglobin has a very sharp decline in it's ability to absorb red and near-infrared which indicates hemoglobin evolved specifically to allow these wavelengths to pass through. The CCO pump has a longer evolutionary history than hemoglobin because it was inherited from bacteria that formed the symbiotic relationship in mitochondria. Decendents of these bacteria still exist as purple bacteria which are used in most research on the CCO pump. 5) Night-time levels of melatonin, but not day-time levels, have been shown by Tiina Karu to completely inhibit the positive effects of infrared light. This indicates that melatonin and its wide swings over 24 hours could have evolved to not inhibit the benefits of sunlight.
In the "test tube", antioxidants nagate the effects of the light, and the light negates the effects of oxidants. In some sense, this may be like the light is an antioxidant.
Details on cytochrome c oxidase: As the CCO absorbs light, its two copper atoms are either oxidized or reduced to transport electrons that are required to help pump H+ to increase the gradient that allows for more ATP. This increases respiration (krebs cycle molecules provide the energy). Calcium Ca2+, alkalinity (0.2 units), and oxidation are increased which causes important secondary responses such as transcription factors that increase DNA and RNA activity. The creation of more ATP increases respiration that increases the production of O-2 oxidation which can be harmful if too much light is applied. Daily moderate use of light therapy induces up-regulation of antioxidants like MnSOD to counteract the harmful oxidation of O2- in a manner much like moderate exercise. Light therapy increases NAD+ which is known to increase endurance as well as increase MnSOD. Over the short-term, heavy exercise depletes NAD+ but light exercise increases it (reference). Light therapy increases GSH (glutathione) which decreases H2O2 that is produced from the extra MnSOD that is converting O-2 to H2O2. Too much wide-spectrum infrared light, such as that received from 3 hours of bright sunlight, causes too much H2O2 which will increase MMP-1 (at least in the dermis of the skin) which some researchers think could cause photo-aging, but not cancer.
By creating an "electron drain" in complex IV (CCO), super oxide O2- may be decreased directly by an electrostatic pull on cytochrome c and thereby on complex III, preventing electron leakage that is believed to result in super oxide O2-. Similar reasoning in the may also indicate an excess of light can actually cause free radicals. The chemical NO is prevented from halting CCO activity and this may explain the immediate pain relief. More electrons being transported to create ATP oxidizes ("alkalinizes") the entire mitochondria, increasing the ratios NAD+/NADH, NADP+/NADPH, GSH/GSSG and signaling important secondary effects such as transcription factors which signal more DNA and RNA. The idea that 600 to 900 nm wavelengths activate cytochrome c oxidase was first proposed 20 years ago by Tiina Karu in 1988. See her 2003 great summary for more about light therapy and CCO.
CCO absorbs energy from 600-900 nm (2.8 eV) photons and reflects them individually with a slightly longer wavelength (approx 50 nm longer), extracting about 0.1 eV of energy in assisting the 0.80 eV (not 0.43 eV) released from a molecule of ATP. If CCO in the body is able to absorb 5% of the 1E17 photons/cm^2 (30 mW/cm^2) in the 600-900 nm range from bright Sun over 0.5 m^2 of skin for 4 hours, then the body has gained 0.030*0.05*5000 cm^2 * 0.1/2.8 = 0.27 watts while using about 100 watts during those 4 hours (0.9 kcalories), making us 0.27% photosynthetic during those 4 hours. The light is directly photo-assisting in the creation of the ATP chemical energy. This does not include the calories absorbed from light that reduces the need for maintaining body temperature.

LED Strength and Dose
Most manufacturers and users of LED devices are underestimating how much time is needed to treat injuries beneath the skin. White skin blocks very roughly 90% to 95% of the incoming light, which most users are not taking into account. Most simple home devices need to be applied for an hour to treat injuries beneath the skin, but manufacturers and users very offten apply them for less than 15 minutes, so the technology works a lot better than most users realize. When injured cells are directly exposed to the light (such as in a test tube or the retina) esearch indicates 4 to 6 Joules of energy (J) applied to each 1 cm by 1 cm area (1 cm^2) once or twice per day is the best dosage. At 10 to 15 J/cm^2, all the ebenfits gained from the light can be negated, so not applying too much light is important. It's really difficult to know how much light gets through any particular person's skin to a particular injury. The best guide is to stop treatment when the pain has been reduced to as much as you expect. If the light is helping a particular injury, the pain will typically be reduced from an 8 to a 2. LED devices specifications should always include W/cm^2 so that the application time can be estimated. However, the LED arrays available are all about the same in terms of effectiveness. Paying more than $2 per standard LED is not needed because the LEDs are the most expensive part and cost only $0.15 each. Manufacturers are powering the LEDs the way they should so that all LED arrays using the standard 5 mm "bullet" type LEDs are the same, emitting 0.010 to 0.015 W (10 to 15 mW) per LED and usual spacing is 2 LEDs per cm^2 (20 to 30 mW/cm^2). A Joule (J) is a Watt (W) applied for 1 second. A watt is voltage times amps. So 6 J/cm^2 is the same as applying an LED device with a strength of 30 mW/cm^2 for 200 seconds (200 seconds x 0.03 W/cm^2 = 6 J/cm^2). The only benefit of stronger LED devices is a shorter treatment time. Ten to 20 times as much energy (Joules) is required to treat tissue that is beneath the skin, or 10 x 6 = 60 J/cm^2 because of the 90% to 95% light (or more) that is blocked by the skin and other tissue between the skin and the injury. For a 0.03 W/cm^2 LED device, 60/0.03 = 2000 seconds = 33 minutes at a minimum. This dosage can be applied twice a day and is not harmful to tissue. Dark skin may require three times more because it blocks very roughly three times as much light. Maybe 500 J/cm^2 is needed to reach injured cells 2.54 cm (1 inch) below the skin (4.6 hours at 30 mW/cm^2). For this reason, typical LED devices are probably not useful for injuries more than 1 inch deep, but to my surprise, they have been useful for knee and shoulder injuries (and are used by professional basketball teams). Higher doses could be dangerous, but I have successfully benefitted from 1,000 J/cm^2 with a halogen spot light supplying red to near infrared at 10,000 mW/cm^2 (100 seconds to get 1,000 J/cm^2).Our ancestors have been exposed to 0.01 to 0.03 W/cm^2 of sunlight in the red to near-infrared range for up to 6 hours a day, giving an average daily dosage in the hundreds of J/cm^2 for very large areas of skin. People with fibromyalgia and arthritis will not a large reduction in pain when the painful areas are exposed to sunlight for a long time. This is strong support for the idea that 1,000 J/cm^2 is not unreasonable in a clinical setting for > 1 inch deep injuries that occur from trauma or surgery. I have found 100 J/cm^2 to reduce pains that are about 1/2 inch deep from an pain level of 8 to 2. I have not observed any harm from 30 minutes of 150 mW/cm^2 (270 J/cm^2) at 850 nm.
LED strength in "mcd" is meaningless. The plastic bulb of LEDs can focus the light to a bright point that has a high mcd rating but as soon as it passes through the skin it's dispersed again as if it were never focused. The important rating is the power per square cm in units of mW/cm^2. A higher mW/cm^2 means less application time is needed. If the manufacturer did not oversize the power supply, the wattage of the power supply should be about 4 times more than the total light energy output of the LED array. The mW/cm^2 is the total light energy in mW divided by the length and width of the array in cm. Your cheek can barely feel the warmth after a few seconds of 30 mW/cm^2 in the 600 to 900 range and 150 mW/cm^2 can make dark skin too hot (> 105 F) after 1 or 2 minutes. Dark skin gets much warmer than light skin from LED devices because the melanin is blocking more of the light, so dark skin requires longer treament time.
Optimum Wavelengths
Certain wavelengths provide a better biological response. In short, CCO absorbs 4 peak areas of wavelengths (see figure below) in the 600-900 nm range that cover almost half of the 600-900 nm range. In an activated state, the CCO changes shape so that even more wavelengths are absorbed. It uses this energy to increase ATP and place the cell in an alkaline or oxidized state that results in many secondary benefits.
From T. Karu, 1996 and 2005
This wide range of wavelengths is specific evidence for the general evolutionary argument that a wide range of wavelengths exactly like the Sun is the best possible exposure. However, there are three ways it might be possible to provide equal or greater benefit than the Sun for hypoxic or injured cells: 1) LEDs can provide injured cells with a larger amount of light in the beneficial range and at times when the sun is not available, 2) we can reduce the heat and thereby provide higher concentrations that reach deeper cells (the Sun is limited to about 1/2 to 1 inch of depth like most LED and laser units), 3) in the future an inexpensive device will be made that is specifically tuned to the CCO set of proteins, having a specific sequence of pulse times of specific wavelengths and pauses, forcing CCO through each step of its pumping action with minimal heat and maximum depth.
A single wavelength may work as good as full spectrum by causing an electrostatic push or pull on neighboring electrons when moving only one electron (into or out of one of the two copper atoms in CCO). The electrostatic push and pull may cascade all the way through the electron transport chain. Complex II activity has been shown to increase even though it does not absorb these wavelengths.
Many different wavelengths have been used, but very few studies have compared different wavelengths. The figure above indicates wavelengths 610-625, 660-690, 750-770, and 815-860 nm are the best wavelengths. Considerations other than how well they activate CCO are: 1) which wavelengths penetrate the best (see section on absorption), 2) which LEDs provide the strongest light output (keep in mind 850 nm has 30% more photons per watt than 630 nm), and 3) possibly 630 nm being usefully absorbed and reflected as (aka "converted to") an 825 nm photon to be used again.
Inexpensive LEDs typically come in 630, 660, 850, and 880 nm with a hard-to-find (expensive) gap between 710 and 830 nm. The peaks of the LEDs and optimum wavelengths are not exact, but spread out about +/- ~10 nm so there is an overlap of available LEDs and the biologically optimum wavelengths. The 630 nm LED can affect the 620nm peak in the chart, and 660 nm LED touches the 680 nm peak, and 850 nm is directly on one peak, but does not cover the nearby peak 820-830 nm as well.

Ability of Light to Penetrate Tissue
Red and near-infrared light penetrate tissue because they are not blocked by blood or water as much as other wavelengths. A doubling of the light intensity at any particular wavelength will double the amount of light energy that reaches a particular depth. Also, doubling the time of application will double the amount of light energy. So if you use a device that is half as strong, you simply have to apply it twice as long. Skin, fat, and muscle all have different absorption and scattering coefficients that change depending on the wavelength which causes this to be a very difficult subject, but the above two simplifying rules are good to keep in mind, as well as the following paragraph that goes into more detail. Knowing how much penetrates to the injury is very important because too little light has no effect, and double the "optimum" amount completely negates all the benefits. But it's impossible for anyone without the proper equipment and time to actually know how much light is penetrating for any particular injury within a factor of 2. So this section will go into detail, but it generally comes down to guidelines I've mentioned elsewhere in this document combined with stopping the light as soon as you see the pain reduction reach a maximum, which is the way I determine "what's best", keeping in mind pain relief may not be equal to optimum healing rate. But more or less, I believe maximum pain relief will be equal to optimum for healing.If a "FRACTION" amount of "INCOMING" light remains after a certain "DEPTH" of tissue, then you can determine the light intensity at a deeper or shallower depth of X*DEPTH (where X is a fraction if it is shallower, and larger than 1.0 if it is deeper than DEPTH). The amount of light at X*DEPTH is equal to INCOMING * [FRACTION]^X. For example, if after 1 cm of homogeneous tissue there is 10% of 830 nm light remaining, then at 2 cm there is only 1% light remaining. If a different wavelength, say 850 nm, has 15% light remaining at 1 cm, then at 2 cm it has 2.25% remaining. Notice that 850 was only 50% better at 1 cm, but more than twice as effective at 2 cm, so light penetration considerations are "exponetially important" for deep injuries. This is mathematically equivalent to the more complicated and detailed example below by the following math relation: e^(-k*cm) = [e^(-k)]^cm = (fraction remaining at 1 cm)^cm where k="effective absorption coefficient". My comments above do not assume the width of the array is larger than the depths under consideration, but the standard "absorption coefficients" discussed below do require this condition if they are to be used in the equations. If the source of light is a point source at the skin like a laser instead of an array, then multiply the "effective absorption coefficient" by 2. This is because point sources of any type of ray, not just light, decrease in strength by an r^2 factor as the strength is diluted as it expands into 3D space. Gravity is a famous example of this geometrical surface area effect.
Example: Applying Light to the Skull for the Brain
There is some research looking into light for diminishing ailments such as dementia and mitochondrial disease. For years I told people it was impossible for these healing wavelengths to make it through the skull. But to my surprise, mainly because it seems the skull is thinner than I thought, the math and research says 50% of near infrared (and very likely red) is able to penetrate 3 mm of skull, out of that light that makes it through the skin. For eaxmple, if 20% makes it through a bald head and skin, then 10% appears to make it to the upper layer of the brain. My intuition can't believe it is more than 25% that makes it through the skull by itself, but for this discussion I'll stick with what the math and researchers say. The equation for percent of light transmitted (assuming the applied array is a few times wider then the depth you want to penetrate) is
mW/cm^2 at depth = mW/cm^2 at surface * 2.718^( - effective absorption coeff * depth)
where (effective absorption coeff) = sqrt(3*A*(A+RSC))
where A = absorption coefficient and RSC = reduced scattering coeff = (1-g)*SC where g is anistropy (average cosine of scattering angle) and usually 0.8 or higher.
This can be also used with the charts below. For SKULL BONE A = 0.11 1/cm for red and near-infrared < 900 nm and the RSC = 18 although older papers range from 10 to 40 (reference). The skull is about 0.3 to 0.5 cm thick, giving 2.718^(-sqrt(3*0.11(0.11+18)*0.3 cm) = 48% for 0.3 mm and 30% for 0.5 cm of light makes it through the bone, out of the light that makes it through the hair and skin (so bald, light skin people will get a lot more than people with dark hair and skin skin). This is why it is being studied for dementia, alzheimers, parkinsons, and other mitochondrial dysfunction problems in the brain. Out of interest in this, I put together a helmet of LEDs as shown in the picture below to see if I could notice any effects. After 15 minutes it seemed to put me to sleep. Not a deep or long lasting sleep, but just made me tired-sleepy. It's 1,500 LEDs powered by 160 Watts of 660 nm and 850 nm. Light energy was about 40 Watts, 800 cm^2, 50 mW/cm^2. If 5% of the light made it through, that would have been 2 Watts entering the brain. For comparison, the brain uses about 10 watts.

Don't laugh!
Halogen light bulbs for the brain if you place a gallon zip-lock bag of about 1 quart water on your head then place a $10 500 W halogen flood light from walmart within 1 to 3 inches, then you should get a lot of light energy to your brain. When compared in terms of the energy from LEDs and laser, this should provide about 20 watts in the "mitochondria-active" range (1/3 of the 500 W comes out as light like the sun, and about 1/4 of that light is in the healthy range of 4 wavelengths, and about 1/2 of that is wasted in not being on a specific wavelength like the LEDs). The water is to absorb heat. This assumes the head is bald or shaved. It covers about 200 cm^2 so the intensity should be 20/200 = 100 mW/cm^2 which is twice as intense as my helmet but with maybe 4 times less coverage. Maybe I will do 4 of these 500 W halogen surrounding my head with some water blocking contraption. Skin, etc
The question of what percentage of light is allowed through a particular tissue at a particular wavelength is very important, highly varied, and very complex. For example, there are 5 layers in the epidermis and dermis that have distinctly different absorption and scattering properties that change based on the location and color of the skin. All those variables change again based on the wavelength. An even bigger problem is that usable and reliable data to plug into the equations is non-existent. This is the situation for skin, which is always 1 mm or 1 to 4 mm thick, depending on which source you quote.
I have a excel spreadsheet that tries to follow the methods of Steven L. Jacques and The Science of Phototherapy" but it's pretty much useless. Those sources state anywhere from 5% to 50% of the light in the 600-900 nm range is blocked by the epidermis and 5% to 95% is blocked by the dermis, and the only number for fatty tissue I have results in 99% being blocked by 1 cm.
The graph below shows that wavelengths over 900 nm start to get blocked more and more by water.

The graph below shows not much light is able to pass through oxygenated blood (HbO2) when the wavelength is less than 600 nm.

Absorption coeff 1/cm = 1E7 * 4*pi* (extinction coeff unitless) / (wavelength nm). Below is the same data, but INVERTED and expanded in our area of interest.

Below is another interesting graph that shows that each mm of melanin in skin is very effective at blocking light, but that layer is very thin (less than 0.005 cm) compared to the small fiber collagen and hemoglobin in the dermis layer (0.1 cm).

For the best info on HbO and Hb in blood see this. and also S Wray. Even if you understand the math, percent light transmission through tissue cannot be calculated unless you can find the %HbO and %Hb (or mM concentrations) in any particular tissue, along with the "baseline" (no blood) absorption and scattering of that tissue. Do that first and please email me the link(s).
Useful Charts:
Water Absorption Factors, 200 nm to 990 nm
Absorption Factor Chart
Comparing LED Wavelengths
LEDs typically some in certain wavelengths because the material science has discovered specific combinations of elements that results in the best efficiencies. So even if you tried to find LEDs that exactly match what research says are the best wavelengths for tissue response, you may suffer such a large loss in efficiency of the LED to emit light that it does nto make a difference (circuits can get only so hot, given the presence or absence of fans and heat sinks).660 nm verses 850 nm
Wavelengths greater than 800 nm penetrate tissue a little better than wavelengths shorter than 700 (see Light Penetration section). The effect is much larger in dark skin which will benefit more from 850 than from 660. The question is complicated by different wavelengths having stronger or different biological responses. I don't know if one is better than the other, but I currently have a preference for 850 nm over all others. I am in the process of testing other wavelengths to see if I can find anything better than my best 850 device (shown below). 660 nm has a much weaker observed response on CCO, but experiments indicate it works. If 850 nm is better, it might be simply because 850 nm has 23% more photons per mW/cm^2 and CCO is activated on a per-photon basis. (Longer wavelengths have less energy per photon, so equal energy from 850 means more photons). I have not confirmed it, but it appears 850 LEDs are more efficient at emitting light energy than 660 nm and 630 nm, so from a practical viewpoint, circuits of a given style (such as no fan) using 850 nm are simply ABLE to emit more light energy, and LED device businessmen who turn into LED circuit designers, and even professional circuit designers, will not be able to see that the 850 nm spec sheets are saying they can get more light energy out of their circuits than 660 nm designs. The red and infrared spec sheets usually use different ratings (mcd verses mW/cm^2), and it's hard enough adjusting for the "viewing angle" of the LED as it affects the mW/cm^2 and determining if they are talking about 50% level or peak level, not to mention difficulties in conveting with mcd.

When taking penetration and benefits into mind, I do not know if one is better than the other. There are various LEDs in the range of 630 and 660. When I talk about 630 nm, I have 610 to 635 nm in mind, and when I talk about 660 nm, I have 650 to 670 nm in mind. 630 nm red is slightly orange and 660 nm red is a "deeper" red. Since 660 nm is almost infrared, the human eye is not able to see it as well. 630 nm red is used in key rings, traffic lights, and car tail-lights because it's 6 times easier to see than 660 nm (see the photopic response factor - chart ). The eye doesn't suddenly stop sensing light at 700 nm, but it is a gradual decline in sensitivity. You can see the healing and pain relief effect of light therapy by applying a laser pointer or a key ring light to small cuts for 2 minutes or to an arthritic finger joint for 20 minutes.

There are some companies that claim 880 is "the best" frequency, but it appears 880 is absolutely not as good as 850 or 830 nm LEDs. 880 LEDs are putting out frequencies in the range of 870 to 890 and are getting blocked 25% more by water absorption than 850 and the biological response to 880 nm is much less than at 850 nm (see Optimum Wavelengths section).

Measured light output is about 140 mW/cm^2
830 nm verses 850 nm
Judging from the biological response to different wavelengths, it would appear 830 nm is the best of all wavelengths. But 850 nm may be much better for deep tissue as explained below. The 830 nm LED is harder to find, and I don't know if its efficiency is as good as the more common 850. In the end, there may not be any difference between the two.
830 nm is supposed to be better than 850 nm for shallow injuries and possibly better than 850 nm for up to 1/4 inch deep. 850 nm might be better for deeper injuries because more 850 nm reaches deeper tissue. The CCO absorption is the source of all benefit, but 830 nm is being absorbed so well, that it does not make it very deep before all the light energy is absorbed. At some unknown depth, there will be 3 times as many 850 nm photons which overcomes the fact that each individual photon does not work as well as a 830 photon. Mathematically speaking, 830 nm works better by something like 30% but it's exponentially decreasing in strength by something like 10% in the exponential. At some point, the exponential effect on the 10% becomes larger than the 30%. For shallow injuries, 830 nm is definitely working faster, maybe 30% more beneficial, but 850 nm will work just as good if it's applied 30% longer. This means that for the skin or cuts less than 2 mm deep, you would need to apply the 850 nm light 13 minutes instead of 10 minutes for the 830 nm. You save only 3 minutes by using the 830 nm. But for deep injuries more than 1/2 inch, where you might need to apply the 850 nm for an hour, you might need to apply the 830 nm for 2 hours ... a huge difference. A similar discussion is in the 660 nm verses 670 nm section above.
I can definitely feel more heat in my skin from 830 nm devices compared to 850 devices of the same power. This shows more light is being absorbed at a more superficial level. You can feel heat only in the skin, not beneath it, which shows the 830 energy did not make it as deep as 850 nm. At 1/4 inch, 850 nm might be working as well as 830 nm. A 850 nm photon may not be as biologically active as an 830 nm photon at the deeper depths, but at 1/2 inch there may be 2 times more 850 nm photons due to 830 nm exponentially decreasing faster than 850 nm. To see the calculations, review the light penetration section above.
930 nm and above
It appears any wavelength longer than 930 nm will start to have too much of its energy blocked by the water in tissue. See the non-ablative part of the skin section for how 1000-1500 nm can be used to burn the color out of spot and have other beneficial effects.
Blue, Yellow, and Green
See the skin section for information about how blue can help acne (it's really violet, near UV-A) . Blue is about 430 to 485 nm. Green is 510 to 565 nm. Yellow is 570 to 590. None of these penetrate deeper than the skin. See the skin section for how blue can help. There are some companies that claim yellow helps remove wrinkles. I haven't found any research on yellow for the skin that's not conducted by the people who profit from it.

Laser Light verses LEDs
There has been a lot of interest and money in low laser light therapy (LLLT) for healing, but there is no reason to believe that the coherent light from a laser is any better than LEDs, sunlight, or halogen lights. Laser light does not penetrate more deeply and cells, at least beneath the skin, do not know the difference: all photons are the same and the benefits are based on the action of each individual photon, not on bulk properties such as all the photons having the same polarity and coherency. The word "laser" has a superior marketing appeal for companies because it sounds interesting and mysterious. It also costs a lot which means patients can't do it on their own. These are the reasons there has been much more research in LLLT for healing than LEDs and halogens: companies and researchers have expected more profit. Light therapy is ancient and took on various new forms in the 1900's before lasers were invented. At least since 1989 definitive statements were being made in journal articles that lasers are not needed. To quote the most recognized researcher in LLLT, Professor Tiina Karu: "An analysis of published clinical results from the point of view of various types of radiation sources does not lead to the conclusion that lasers have a higher therapeutic potential than LEDs. ...The coherent properties of light are not manifested when the beam interacts with a biotissue on the molecular level....The conclusion was that under physiological conditions the absorption of low-intensity light by biological systems is of purely noncoherent (i.e., photobiological) nature....specially designed experiments at the cellular level have provided evidence that coherent and noncoherent light with the same wavelength, intensity, and irradiation time provide the same biological effect. Successful use of LEDs in many areas of clinical practice also confirms this conclusion." (Biomedical Photonics Handbook, 2003). Thankfully, Dr. Karu is a Russian Professor so we can expect her research to be more honest and scientific compared to U.S. medical research based on corporate profit. From a journal article: "...according to all available data, does not depend on the coherence of radiation." Reference: "Photobiological Principles of Therapeutic Applications of Laser Radiation" published by Yu. A. Vladimirov, et al in Biochemistry (Moscow) Volume 69, Number 1 / January, 2004.Sunshine
Bright sun at midday in the southern U.S. in summer has as much energy in the red and near-infrared (600-900 nm) as LED arrays (about 29 mW/cm^2 - see chart below which has an error in saying '39'). But only about 50% of the light in the 600-900 nm range from the Sun is at the best wavelengths, so it requires mirrors and sunscreen to increase the amount of Sun to equal the best LEDs devices which have all their energy concentrated at the best wavelengths. If mirrors are not used, treatment time is doubled or tripled to get the same benefit as a good LED device, but then getting hot becomes a problem if you don't have a fan and a mist of water to keep cool.

Halogen Lights
Halogen lights are the strongest and least expensive method of obtaining light therapy, having approximately 35% of it's light in the 600 to 900 nm range. I often use a 75 W halogen spotlight size PAR30 from Lowes and an empty snow globe filled with water to block the far-infrared heat (see picture below). The 75 W light is powered by a lamp cord that has a switch in the base. There are several dangers to this, so I do not recommend anyone try it without strong caution. For example, the snow globe can focus the light too strongly and quickly burn the skin. The super-bright white light from the reflection off the skin can damage the eyes, so I have to wear sun glasses. The base gets hot, and setting the light down can burn tables and carpet. Dark skin burns very easily with this because it blocks all the visible light energy in the surface of the skin, concentrating the energy in a small volume of tissue. A slightly safer and less extreme set up would use a halogen flood light instead of spot light and a zip-lock bag filled with 1/2 inch of water when laid flat (instead of the snow globe).Light Therapy Bed After reading my comments about using halogen lights as a "healing" bed and for the winter blues, someone in Canada in winter 2007-2008 did a great job of implementing the ideas. I had a picture here of my "light bed" and he copied it, doing a better job (see picture below). It uses $5 full-length mirrors, $5 halogen 500 W flood lights, pyrex glass baking pans, and food coloring. The water in the pyrex pans is to block the far-infrared heat. A lot of light energy comes through which warms you up. The food coloring in the water in the pyrex pans blocks visible light energy but still lets the red and infrared through. He actually found the spectrum from the manufacturer of the food coloring which showed the proper wavelengths are allowed through. The food coloring is probably not needed (I wasn't able to tell much difference in the heat, and the Blue/green/yellow wavelengths might be god for the skin). The six 500 W flood lights use a total of 3,000 Watts and would need to be on two different electrical circuits in most U.S. houses without tripping a breaker. It's very calming and can put you to sleep quickly as if you're on the beach....it definitely feels as if you're on the beach. The only bad thing is that there is no U.V. for generating vitamin D which could prevent 50% of breast, colon, and prostate cancers in the U.S. - skin cancer is unimportant by comparison.
2010 update: He emailed: "About 20 minutes on my back then 20 face down.... Kind of makes me really relaxed and sleepy too . . . similar to eating turkey."
2011 update: He reports: "It heals scars and keloids - not immediately, but gradually. Also moles disappear over time, even ones I've had from birth."
Email pictures to me at scott@heelspurs.com if you build a similar set up, and email me after a month and once a year to let me know how it's going so I can post results here.

What would it take to do this with LEDs? To cover from the knees to the face, top and sides, about 10,000 LEDs running at 50 mW each with normal spacing of 2 LEDs/cm^2 (12 LEDs/in^2). Power supply would therefore be 500 W. With fans, you can run the LEDs at almost 100 mW each and use half as many (spaced further apart). The 5,000 LED array shown above (with my black New Balance shoe) cost $750 for the LEDs. Someone on alibaba.com is probably already selling this type of healing bed. They should target the 15,000 tanning salons and 50,000 chiropractors in the country. Email me if you find a good one.
Halogen lamps will produce light like the Sun and it can provide more light energy in the healing (tissue penetration) range of wavelengths than regular incandescent and heat lamps. This will be much more energy than LEDs can provide and the energy will be spread out over a larger range of wavelengths (see chart above comparing LEDs and Sun). The halogen is closer to the Sun's natural spectrum. Halogen lamps usually have glass covers that block UV light so that desk lamps do not cause sunburn to hands. The strong blue wavelengths of halogens can be very harmful to the eyes. As with typical LEDs that have about 20% efficiency in converting power input to light output, and as with the wide-spectrum of the sun, halogen lamps also put out about 28% of the energy they use as light energy in the tissue penetration range. So a 75 W Halogen spot-light that concentrates 80% of its light in a 10x10 cm area will produce 75*0.80*0.28/10^2= 0.168 W/cm^2 = 168 mW/cm^2 of light intensity in the tissue penetration range, but the heat from the far-infrared in the skin will be too powerful to keep it there for more than a few seconds. This is about 3 times the best LED array and 5 times the healing range of sunlight. About half of this, 84 mW/cm^2, is near the four specific beneficial wavelengths. To get as much light from a halogen as from the sun, you can compare the heat you feel from a halogen to the heat you would feel from the sun and the healing dosage should be almost as much. Plexiglass can block some of the far-infrared that heats the tissue. Well-designed LEDs will not have the heat problem at all and are not supposed to be harmful to the eyes (I'm still researching it) which are two important reasons they are being used. LEDs are more powerful over a short range of wavelengths which appears to be just as beneficial as having the wattage spread over a wider range of wavelengths as occurs with halogens and the Sun.
Halogen lights contain a lot of blue light and are very dangerous to the eyes.

Comparing halogen, incadescent, heat lamps, and the sun:The Sun, Halogen lamps, incandescent lamps, and infrared heat lamps all emit light based on the black body radiation principle (see this excel spreadsheet if you want to calculate energy in a specified range of a black body spectrum). Halogen lamps have a curve half way between the ones shown for incandescent and the Sun (see this chart). The Sun and halogen lights have about 28% of their energy in the 600 to 900 nm range. Incandescents have 15% to 21% and heat lamps have about 10%. To produce light, halogen, incandescent, and infrared heat lamps heat up a spiral filament of tungsten metal. The filament "incandesces" which means it produces light by black body radiation. A halogen gas can allow the filament to get hotter than regular incandescent bulbs. Heat lamps are the same as incadescent lamps but their long filament is operating at a cooler temperature so that it produces more far-infrared. They operate at approximately the following temperatures: Sun - 5780 K, halogen - 4100 K, incandescent - 2800 to 3200 K, heat lamp - 2400 K. Energy in the far-infrared is easily absorbed by water in the skin, concentrating the light energy in the skin that causes pain from heat sensors.

Skin: Wrinkles, Acne, Scars, and Spots
I have historically been against the idea that LEDs might help skin for anyhting other than recent wounds. There appears to be only one good article that disagrees with me in the case of sun-damaged skin (see this). But for now, I will retain my old, skeptical comments about LEDs and skin, as can see in the rest of this section.Simple LED devices for use at home do not work on wrinkles, aging, or scars. Wrinkles are old, fixated collagen, like scars. LEDs repair recent injuries in cells that need more energy. This is the only way they work. There is no reason to believe this will reduce existing scars or wrinkles. Pictures of wrinkles before and after are not comparable because the angle of the lighting and the amount of smiling drastically changes things. I found only one journal article (see below) that indicated simple red and infrared light energy can help.
Low Power Devices for wrinkles and aging:
- This article on aging skin (primarily wrinkles caused by photodamage) reported red (633 nm at 126 J/cm^2) and near-infrared (850 nm at 66 J/cm^2) for two treatments per week for 5 weeks resulted in 67% of the patients reporting good to excellent results in softness, smoothness, and firmness.
- There's an FDA-approved "Titan" device that uses strong infrared to tighten skin, available only through a doctor.
- I saw an article claiming pulsed blue was good for wrinkles, but the research was so bad, I'm not providing the link.
- See also non-ablative below (medium power devices that require a doctor visit)
Spots:
Non-ablative devices are not as serious in terms of risk as ablative (destructive) and they may soon be as good as the older ablative techniques. The non-ablative devices usually use high-energy focused spots of laser light that cannot be duplicated by LED devices sold on the Internet. Wavelengths from 500 to 3000 nm (blue to mid-infrared) have been used, but 1000 to 1500 is being researched the most. These techniques are improving, but are still not as good as ablative. Usually, between >1000 nm and < 1500 nm wavelengths, long or short pulsed, are used to heat the water in the skin to cause heat damage to the cells. Therefore this technology is much different than the 600-900 nm healing wavelengths that the rest of this page is concerned with. Studies have used three to eight treatments typically one month apart. Cryogenic cooling may also be used to minimize harm. At Reliant Technologies, the ablative areas are a about 0.5 mm deep into the skin and twice as thick in diameter as a human hair. "Fractional rejuvenation" or "fractional photothermolysis" is the non-ablative version of the grid pattern used in ablative techniques.
Fractional photothermolysis (FP) has been recently introduced as a new concept in dermatologic laser medicine. FP employs an array of small laser beams to create many microscopic areas of thermal necrosis within the skin called microscopic treatment zones (MTZ). Even though FP completely destroys the epidermis and dermis within these MTZ, the 3-dimensional pattern of damage heals quickly and with few side effects. FP is currently used to treat fine wrinkles, photodamaged skin, acne scars, and melasma. Due to its clinical efficacy and limited side effects FP has established itself in the past two years as an alternative treatment modality to the conventional ablative and non ablative laser therapy. 2007 German articleAnd here's another review from 2006:
Ablative lasers (CO2 and Er:YAG) provide the greatest improvement in photoaging, but significant adverse effects limit their use. Nonablative lasers have reduced adverse effects, but limited efficacy. Fractional photothermolysis (FP) produces arrays of microscopic thermal wounds called microscopic treatment zones (MTZs) at specific depths in the skin without injuring surrounding tissue. Wounding is not apparent because the stratum corneum remains intact during treatment and acts as a natural bandage. Downtime is minimal and erythema is mild, permitting patients to apply cosmetics immediately after treatment. As with other nonablative laser modalities, multiple treatments are required. FP represents an alternative for treatment of dermatologic conditions without the adverse effects of ablative laser devices and can be used on all parts of the body. FP can be used for the treatment of facial rhytides, acne scars, surgical scars, melasma, and photodamaged skin.To quote an outdated 2002 MedScape article to show the initial skepticism of non-ablative techniques 6 years ago:
Unfortunately, clinical data in support of nonablative lasers and light sources [including LED devices] for wrinkle and acne scar treatment remain unimpressive. Despite a series of lectures and dozens of research presentations dedicated to the subject, results at this year's ASLMS often failed to impress the audience. Some before-and-after slides elicited puzzled expressions, while others triggered sporadic laughter. As one attendee murmured during a presentation, 'I can't tell any of the befores from the afters.'Since this quote, many postive articles have been published. One study used 14 J/cm^2 with a 0.3 ms short pulse at 1064 nm for improving scars. Another used a combination of blue and infrared: 7 to 15 J/cm^2 with 7 to 50 ms pulses at 535 nm and 24 to 30 J/cm^2 with 30 to 65 ms pulses at 1064 nm. 1300 nm and 1500 nm lasers are also commonly used.
- Abstract 4, 2007 Braun (flourescent and high-pulse non-ablative)
- Abstract 5, 2007 Alster (radiofrequency non-ablative)
- Abstract 6, 2007 DeHoratius (laser, infrared, and pulsed, all non-ablative)
- Abstract 7, 2006 Ruiz-Rodriquez (non-ablative)
- Abstract 8, 2004 Kim (non-ablative not yet as good)
- Abstract 9, 2005 Freedman (combining ablative and non-ablative)
- Abstract 10, 2004 Tanzi (1300 and 1500 nm non-ablative, scars)
- Abstract 11, 2007 Keller (1064 nm non-ablative, acne)
- Abstract 12, 2006 Lipper (1064 nm non-ablative)
- Abstract 1, 2007 Mezzanna (ablative)
- Abstract 2, 2007 Ruiz-Rodriquez (ablative)
- Abstract 3, 2007 Jih (ablative)
- Abstract 13, 2003 Lee (combining 535 and 1064 nm)
Treating the Retina
Read this section at your own risk. I am not a doctor. The safety issues are complex as can be seen in the safety section below and I often make mistakes.LED light helps only cells that are injured, not dead cells nor scar tissue. Red and infrared LED arrays may help macular degeneration, retinal tear, and laser burns, but very probably not floaters. They could possibly make floaters worse. They are best at treating injuries that have occured within the past few days (the sooner the application, the better). This means about 300 seconds of a typical 25 mW/cm^2 array which is the max officially allowed for infrared before it supposedly heats the lens and cornea. I could not find any information that indicated any normal 5 mm type LED in red could ever hurt the lens or cornea, so you can apply red for longer time periods, but because the pupil response is to become smaller, red is blocked about 5 to 10 times more than infrared, which means it would need to be applied 5 to 10 times longer. My experiments indicated (see pictures below) 5 times more because the area of a 5 mm pupil is 5 times more than a 2.3 mm pupil. I have applied 150 mW/cm^2 850 and 830 nm for 3 minutes several times and did not notice any harm, which is 3 times more than is needed to treat the retina. I believe the ideal array for treating the eye will be 25 mW/cm^2 at 830 nm for 300 seconds while being moved around (definitely not kept still where the retina might be heated too much). 850 nm may work just as well. See the Safety section below on "Retinal Heating" for more information on trying to treat the retina. Especially example 4.



Safety Concerns
Halogen lights contain a lot of blue light and are very dangerous to the eyes.Typically, there are no safety concerns for LEDs unless they are blue or they are really strong or applied directly to the eye.
Heating the Skin
Leaving LED devices on too long and wrap tightly against the skin is probably the most likely cause of harm. Skin temperature should never be more than 41 C (105.8F) to meet FDA regs. Even a weak LED array will cause 2nd degree burns if it is wrapped snuggly with an ace bandage under blankets because the heat is not being allowed to escape. No matter how "cool" a heat-producing device operates, if it's wrapped good enough and long enough, it can get hot. I've found around 0.7 Watts per square inch to be the maximum energy that can be put into a device that touches the skin without a fan or special heat sinking, and even then it will cause 2nd degree burns if there is not an automatic off at 15 minutes and it is wrapped tightly and left in place for over an hour.
Eye Safety
Strong blue and white LED's harm the eyes! Strong green LEDs have 1/15th the risk of blue. Strong and focused Red and yellow LEDs appear safe for at least 5 minutes, as long as they are not the really strong kind like 1 watt and applied directly to the eye.
The ACGIH does not have a safety factor specifically for simple LEDs (as of the last booklet I have which is 1996) because they appear very safe. But it has guidelines to prevent damage to the lens and retina from any light source. The TLV for laser light doesn't apply to non-laser LEDs because lasers are different because they focus the light energy in one spot which is much more likely to cause harm. Blue LEDs may harm the eyes from a photochemical injury called the "blue light hazard" (aka "solar retinitis") that can cause temporary or permanent loss of vision wherever the blue light strikes the retina. This is very dangerous and blue LEDs as key rings should be against the law. Blue is 1,000 times more dangerous than near-infrared of 890 nm (see pdf below, page 5). Red, yellow, and green also have photochemical risks, but only green has the remote possibility of causing harm (if it's high power with a narrow emission angle). Beach and snow always need dark sunglasses for protection against UV and blue damage, and over the long term it helps prevent cataracts from the infrared wavelengths. UV is the most dangerous because it has stronger photons than blue and violet.
Red, yellow, and green are very safe as long as the power is not so high that the retina heats up (this may cause floaters or other less serious "silent" injuries, but I do not have a erference). For yellow, green, and most reds, it will be clear the light is too bright before any harm occurs, unless it is laser light.
Do not assume any of these statements are true when dealing with LEDs. Use this information your own risk.
Lens and Cornea Harmed by Infrared
Cataracts are the more likely source of harm from non-laser, non-blue light, and it occurs from near-infrared and far-infrared (> 770, but < 3,000 nm), but not red. If you work outside or in front of an oven all day for years without eye protection, you are slightly more likely to develop cataracts (in the lens). See long quote below. Glass and thick plastic (safety glasses might be too thin) block far infrared (steel workers) and sunglass for the beach and snow that are not too weak and orange-tinted will probably be OK for the red and near-infrared heat energy. The ACGIH TLV guidelines say infrared eye exposure to prevent injury to lens and cornea should be less than 10 mW/cm^2 if it's greater than 15 minutes. For less than 15 minutes, the TLV guidelines says mW/cm^2 should be < 1800 mW* (seconds)^(-0.75). This equation means that for a typical 25 mW/cm^2 infrared LED device, it's safe to apply up to 300 seconds. These equations overstate the risks of 770 nm to 850 nm from LEDs because the lens and cornea in this range absorb roughly 5 times less energy than longer wavelengths (see links above). Similarly, water and plastic do not hardly block 770 to 850 nm compared to > 850 nm (see charts above). This means 770 to 850 nm make it to the retina seemingly as well as red, which means, like red, they have less energy that can harm the cornea and lens. Red carries even less risk for the cornea and lens. The cornea is the outer covering of the eye that has a bump. It is most sensitve to far infrared such as facing a fire (> 1,300 nm). Closed eyelids protect it. For comparison, staring down at perfectly white beach sand filling your field of vision at noon emits about 25 mW/cm^2 in the near and far-infrared. This is very close to what a typical infrared LED array will emit (including infrared security camera night illumination arrays and infrared flashlights). Devices with fans can acheive 200 mW/cm^2 (like devices I've made for myself: see picture with blue-plastic LEDs way above). I meantion the beach and snow infrared intensity (not counting their UV's and blues) to show that the guidelines indicate they are dangerous even in the infrared, but also to remind you that blue and UV is more dangerous, and to show that the guidelines give more protection than being on the beach for 10 minutes.
Near-infrared thermal hazards to the lens (associated with wavelengths of approximately 800 nm to 3,000 nm) with potential for industrial heat cataract: The average corneal exposure to infrared radiation in sunlight is of the order of 1 mW/cm^2. By comparison, glass and steel workers exposed to infrared irradiances of the order of 80 to 400 mW/cm^2 daily for 10 to 15 years have reportedly developed lenticular opacities (Sliney and Wolbarsht 1980). These spectral bands include IRA (700-1400 nm) and IRB (1.4 �m-3.0 �m). In contrast to blue light, IR-A is very ineffective in producing retinal injuries (Ham, et al., 1982, 1976). The American Conference of Governmental Industrial Hygienists (ACGIH) guideline for IRA exposure of the anterior (front) of the eye is a time-weighted total irradiance of 10 mW/cm^2 for exposure durations exceeding 1,000 s (16.7 min) (ACGIH 1992 and 1995). Pitts, et al. (1979) showed that the threshold radiant exposures to cause lenticular changes from IR-A were of the order of 5,000 W*s/cm2.Retinal Heating
This is not an issue for most red and near infrared LEDs, but I need to go into detail because people are applying LEDs directly to the eyes and the information is hard to find, even harder to understand, and this is the only page that shows how to apply the equations to an infrared array (it took me several days to figure it out and type everything below). The retina can be harmed by all visible light and near infrared, but not by far infrared that is blocked by the lens, cornea, and liquid in the eye. Internet references and even books are very poor at explaining the light intensity on the retina, so I'll go into painful detail. There is a discrepency on basics like the eye's focal length. Is the focal length 1.7 cm or 2.2 cm? It's not fixed like most web sites assume because it increases from about 1.7 to 2.2 cm as you focus on objects further away, not counting differences for different size eyes (although different size eyes also have larger pupils so the effect cancels). If you're over 40, about 20 cm is about your shortest focus which gives focal length = 2.2 as lowest value. It's important, because (2.2/1.7)^2 in the equations means 67% higher intensity on the retina if it's 1.7. Someone really near-sighted might have a focal length of 1.4, if I understand it correctly, which would be 2.5 times more light intensity on their retina than others for some of these calculations. Pupil radius increases the light intensity on the retina by a factor of 12 as it changes from dark indoors (0.7 cm) to bright outdoors (0.2 cm), but when I applied 850 nm infrared devices which show a slight red glow (see pictuer above), my retina dilated to only 0.53 cm, which is the max I'll use in the equations.
Equations
All the following assume the light rays are not parallel or converging, but diverging. Steridans measure the "AREA" of a sphere's surface in the same way degrees measure the "LENGTH" of a section of circle. There are 360 degrees in a circle and 4*pi steradians in a sphere. Mathematically:
Steradians = 2*pi*(1-cos(1/2 angle of emission)) = 4*pi*[sin(1/4 angle of emission)]^2 and for small angles = pi*(half angle in radians)^2. Angle of emission in radians as seen at a distance = diameter of source/distance to source.
X = radiance in mW/cm^2/Steradian where the surface areas we'll use for the light source and the receiving object are facing each other and not tilted (so a cosine angle adjustment is not needed).
(1) X = (mW of light source towards receiver) / (cm^2 area of the LED die or light filament as *observed* by the receiver) / (emission angle in steradians towards receiver of the given mW)
X is "radiation intensity" or "spectral radiance" and is very confusing, but very useful because it is the light "radiant flux" (watts) through a surface area that does not change as you get further from the light source, so it is a wonderful constant for a given light source. It is irradiance ( W/m^2 or mW/cm^2) divided by the steridians of the meters^2 at where the watts were measured. The steridians of the meters^2 measurement location depend on how far the measurement location is from the initial source of light.
(2) X = (mW emittedl) / (cm^2 *apparent* size of the light source) / [ 4*pi*(sin(1/4 of emission angle of the mW))^2 ]
angle of emission = 2*arctan(diameter of a distant cm^2 the light passes through / 2 / distance to light source)
(3) X = (mW / cm^2 ) * 1/pi * (distance from source)^2 / (radius of source)^2 assuming the source is small such that sin(radians)~radians and mW/cm^2 is measured at the "distance from source".
(4) (diameter of spot on retina) = (diameter of object) * (inside eye diameter = 2.5 cm) / (distance to object)
(5) 1 / (focal length) = 1 / (inside eye diameter = 2.5) + 1 / (distance from light source to pupil)
Assume (inside eye diameter) = 2.5 cm
eye focal length ~ inside eye diameter ~ 2.2 cm unless it is a young person focusing close, or someone really near-sighted. Not 1.7 cm which is "object focal length".
"Angular subtense" of object being viewed = degrees in field of view = 2*arctan(height/2/distance)
k = fractional amount of light the eye does not block before getting to retina. About 0.90.
(6) mW/cm^2 on retina = X * pi * (pupil radius)^2 / (focal length)^2 * k
(7) mW/cm^2 on retina = mW/cm^2 * (area of pupil) / (area on retina the light is striking) * k
(8) mW/cm^2 on retina = mW/cm^2 / [ 4*(sin(1/4 emission angle))^2 ] * (pupil radius)^2 / (focal length)^2 * k (note: pi in numerator and denominator cancelled)
(9) mW/cm^2 on retina = mW light / (apparent cm^2 area of the LED die or light filament) / (emission angle in steradians) * (pupil radius)^2 / (focal length)^2 * k
(10) mW/cm^2 on retina = mW of laser / area of spot on retina = mW / (pi * (1/2 radian divergence of beam * eye focal length)^2).
This simple last equation works because laser enter in an area that is smaller than the pupil.
Note: given a die size and the watts emitted from the LED, I could not find a way to properly estimate the important X in mW/cm^2/sr it is emitting. For example, say a 0.01 cm^2 die is emitting 300 mW light (i think this is about right for some 1 W LEDs possibly being run a bit hot - the manufacturer maybe should have used a larger die). Right at the surface I can estimate 1/3 of the 300 mW is coming out the front of the die directly, and the steridians for that "half sphere" is about 6, so this gives 100/0.01/6 = 1,700 mW/cm^2/sr, but I don't know how accurate this is, and I don't know how to do it more accurately. It might be off a factor of 2. If the die were a sphere with 0.02 cm^2 surface and emitting 300 mW, then it would be easier: 300/0.02/(4 pi steridians) = 1,200 mW/cm^2/sr. A flat die seems like it should be a little better at directing in a more forward angle, so my 1,700 makes sense. LED lenses seem to not increase mW/cm^2/sr as much as you would think (and maybe not increase it at all) because they increase the apparent size of the die which increases the cm^2 in the denominator even as the mW being directed into a tighter angle is increased.
Example 1:
Take a typical 5 mm type 850 nm infrared LED that outputs a typical 15 mW of light from 50 mW power input. Its plastic case is a little sharper than many, outputting 75% of the light energy into only +/- 10 degrees. What is the mW/cm^2 of the light on the retina at 1 cm away from the eye? At 10 cm? How big is the image created on the retina? How many cones is it hitting?
To answer this, I first need to know how big the LED light source APPEARS after being focused. The die in this LED measures about 0.033 cm on a side which is 0.001 cm^2 area, but this is not what I need (BTW, 100 W/cm^2 die seems to be what a lot of LEDs can be operated at, with 1,000 W/cm^2 peak pulses). The area it APPEARS is a function of how much it has been focused, and I don't know to calculate that from the emission angle. And the LED die sits in a bowl reflector that is reflecting the sides and bottom light from the die. So instead of trying to use guesstimate math, I'll use guesstimate observation and take a picture of this LED in operation (see below, note: total area is 0.055 cm^2, not 0.10, even though I crossed it out). The light shows a lot better in the camera than the dim red that you can see with the naked eye. The radiant intensity is:
Eq (2): X = 15*0.75 mW / 0.055 cm^2 / ( 4*pi*[sin(20/4)]^2 ) = 2145 mW/cm^2/sr
Assume a typical focal length of 2.2 cm (it's not someone under age 35 who is focusing less than 20 cm nor someone strongly near sighted) and a dark room to let more LED light in so pupil radius = 0.6/2 cm.
Eq (6): mW/cm^2 on retina = 2145 * pi * (0.3)^2 / (2.2)^2 * 0.90 = 110 mW/cm^2 at all distances, which provides a nice 6 J/cm^2 treatment in 55 seconds.
Width on retina of the image at 1 cm and 10 cm:
eq (4): width = 0.16 cm * 2.5 / 1 = 0.4 cm
eq (4): width = 0.16 cm * 2.5 / 10 = 0.04 cm
A length of 0.04 cm * 3,800 cones/cm = 150 cones
Notice image size on retina is the only thing that depends on distance. So the image gets smaller as the LED is further away, but the intensity of light per cm^2 does NOT. So if the intensity were dangerous to individual rods and cones like blue or UV light, then it does not matter how far away you get, cells would still be injured. This is long as the diameter of the image on the retina is larger than 1 rod or cone (a 0.2 cm arch weld from eq (4) covers 1 cone at 66 feet but I have not verified this).

Example 2:This is a lengthy and wide-ranging "example" is more of a discussion and illuminatino of complicating factors that ends with an example. My infrared LED emits from the front surface the 5 mW per 0.033x0.033 cm die. 5 mm LEDs can often be pulsed with 10 times higher amps with a 10% duty cycle (others like SMD and super bright can pulse only 60% higher), but the rods and cones are not likely to know the difference with pulsing because they require heat build-up to "melt" just like the semiconductor, so it balances out in terms of safety (and how strong the light appears). It appears 1 W LEDs have dies about 0.1 cm wide and at 30% efficiency, they might be emitting 300mW/0.1^2 = 30,000 mW/(die cm)^2. Coming directly out the front surface might be half of this, 15,000 mW/cm^2 die, which is 3 times higher than my infrared LED. This makes sense: the 5 mm LEDs can't be run as intense continuously per die area, but can be pulsed higher. This implies the 5 mm LEDs can't dissipate heat as fast and that the peak pulse of amps depends on the die area. So it appears the 50 mW 5 mm LED and the 1,000 mW white LED can reach similar max temperatures and similar max peak watts per cm^2 of die area. This has importance in trying to understand generalizations about the safety of LEDs in terms of thermal effects on the retina (I will not discuss blue hazard because it is more clearly dangerous and things are complicated enough trying to determine red and infrared safety). Getting back to this "example", let's assume no LED plastic cover is converging the light on a spot smaller than the die area itself but only directing the light forward that would normally get lost to the sides. So at max it is a perfect laser who's beam is not diverging even a little like normal lasers. LED focusing can't be nearly as good as lasers and even lasers can't be exactly parallel rays, but I want to look at most intense case for LED dies. Let's say the die is infinitely wide and tall and there's no focusing (rather, instead of focusing to make it equal to the worst case of non-converging focusing and easy to calculate). This is a "worst case" for safety by trying to make it maximum intensity. Focusing can't be stronger than this unless the focusing is converging the rays onto a point rather than simply directing the light in a more "forward" direction. This does not increase the intensity of the light per cm^2 PER DIE AREA as it appears on the retina because that type of focusing (non-converging) makes the die APPEAR bigger as in example 1 (as the mW increases from focusing, the apparent die aera increases, so there is no net radiant intensity increase: mW/cm^2 of die area I think might be a constant). So an LED casing is more like a microscope which needs more light on the object to see it because the objective lens is small compared to your pupil but not like a telescope which has really large optics to focus DOWN the light into your pupil. Getting back to this example's theoretical infinitely wide and tall die, there is a rule that says for a flat plane emitting any type of rays per cm^2 like light, sound, or gravity the strength will not diminish over distance. This is because as it tries to get weaker with distance, contributions from the sides increase to balance it out. So the mW/cm^2 of the die will be the mW/cm^2 that your pupil sees. Let's guess that no commerical LED die constantly emits more than 30,000 mW/cm^2 per die area, and so the pupil will see 30,000 mW/cm^2 (no steridians in denominator because I tricked it to go away with an infinte die) from this huge die. This is 300 times the strength of the Sun but it covers the entire the font field of vision rather than a single spot like the Sun. The Sun is 0.53 degrees instead of 180 degrees which is 100,000 times less surface area (steridians) of the emission source. So, the die is 300 times stronger mW/cm^2, but coming from 100,000 times more surface area, giving 300/100,000 = 0.003 times less "radiance" (radiant intensity mW/cm^2/sr) that is important in terms of intensity as a spot on the retina. Said another way, this very large LED's 30,000 mW/cm^2 hits the pupil, and it SPREADS OUT across the much larger retina area. The pupil's hole is at most pi*(0.7/2)^2 = 0.38 cm^2 (infrared LEDs would allow this) letting light through and the retina is about 13 cm^2, so the average intensity should be roughly based on this ratio of areas: 30,000 * 0.38 / 13 = 900 mW/cm^2 on the retina. More precisely, using the focal length and equation (8), I get 341 mW/cm^2 so the method of simply dividing by the area of the pupil by area of retina is a 2.5x over-estimate. Eq (8) for the Sun's 100 mW/cm^2 gives 106,000 mW/cm^2 spot on the retina. Dividing 341/106,000 = 0.003 less from the LED as predicted above. But using a better number for the pupil radius as in the next example gives a much lower 8,700 mW/cm^2. A small change in pupil radius can have a large effect because it is a squared factor. 8,700 / 341 = 25, meaning the Sun is roughly 25 times worse on a spot of retina than the most massive and dangerous red or infrared LED I can imagine. Since the small spot from the Sun dissipates heat better, the safety difference is actually much less than 25. Once the correction for "retina heat dissipation" is made, such a large LED die is more dangerous than the Sun, and for the entire retina, not just a spot.
Example 3:
Sun, eye focused at a distance (focal length=2.2 cm), bright outside (pupil radius = 0.2/2). Sun insolation is 100 mW/cm^2 and is 0.53 degrees in the sky:
Eq (8) mW/cm^2 on retina = 100 mW/cm^2 / [ 4*(sin(0.53/4))^2 ] * (.1)^2 / (2.2)^2 * 0.9 8,700 mW/cm^2
This heat energy is the upper bound of what is safe for 1 second exposure. The real danger from the Sun is the blue and UV which are not part of the considerations in this section. We are designed to cope with the Sun in our peripheral vision for most of the day. This gives an idea of how safe red and infrared LEDs.
Example 4:
Apply a 25 mW/cm^2 from a typical 850 nm infrared ARRAY to the eye in a dark room. In order for this calculation to be more accurate, the array needs to be far enough away that the LEDs appear similar in strength which indicates their light beams are overlapping. If the array is close and the emission angle is small, then only 1 LED will appear bright for a very small section of retina and you would just use example 1 for that 1 LED. For an array, you are not getting a nice and even mW/cm^2, but you get an array of spots on the retina where each spot corresponds to example 1 (75 mw/cm^2 per spot). So to get an even treatment, the array should be moved in tight little circles. The tighter-angle LEDs will have to be further away to appear the same strength, which means the array has to be wider to cover a large area. The following is for 25 mW/cm^2 850 nm array, at +/- 15, +/- 10, and +/-5 degrees emission angles, a dark room (0.6 pupil), and not trying to focus at a close distance ( 2.2 cm focal point):
Eq (8) mW/cm^2 on retina = 25 / [4 (sin(5*2/4))^2 ] * (0.53/2)^2 / 2.2^2 * 0.9 = 43 mW/cm^2
Eq (8) mW/cm^2 on retina = 25 / [4 (sin(10*2/4))^2 ] * (0.53/2)^2 / 2.2^2 * 0.9 = 11 mW/cm^2
Eq (8) mW/cm^2 on retina = 25 / [4 (sin(15*2/4))^2 ] * (0.53/2)^2 / 2.2^2 * 0.9 = 4.5 mW/cm^2
These numbers are only if the array is being moved around in the field of vision. If stationary, then use example 1 for each spot the array creates on the retina. The 11 mW/cm^2 for +/- 10 degrees is 10 times less than for a single LED kept still as shown in example 1. This implies the "no-light" area where there is not LED light from the circuit board as seen by the eye is 10 times the area of the light seen coming from the individual LEDs. In example 1 I observed the LED light per LED covering 0.055 cm^2. I use these LEDs to produce 25 mW/cm^2 arrays and I space them 2 LEDs/cm^2. So the light is coming from 2 LEDs (0.11 cm^2 of light) per 1.0 cm^2 of circuit board space, a factor of 10 difference, right in line with these calculations.
For a red LED, the pupil will be 0.23 cm instead of 0.53 cm giving: 7.4, 1.9, and 0.8 mW/cm^2 which is very small.
If I were treating my retina I would use an infrared array with +/- 5 or +/- 10 degrees LEDs. Treatment time is to get about 6 J/cm^2. For example, at 25 mW/cm^2 with +/- 10 degree LEDs, retina gets 11 mW/cm^2 which would be 6/0.011 = 545 seconds = 9 minutes as a max, maybe 3 minutes as a minimum that may be enough to get good benefit. More than 10 minutes may start reducing the benefits. According to the TLV safety guidelines below, more than 5 minutes is not safe for the lens and cornea at 25 mW/cm^2 at 850 nm, but I believe they are being too strict for this wavelength as detailed above. It will be hard to know how many mW/cm^2 an array is supplying unless an experienced person looks at the operating array, or if the manufacturer actually knows his specs rather than guessing from data sheets. 25 mW/cm^2 will be what a good security camera illuminator array from ebay will provide, given that they use 5 mm LEDs spaced about 2 per cm^2 and you can easily see the red glow from the 850 nm LEDs in a lighted room. There is a section above that shows how to measure it if the measurement is done carefully and correctly. The retina does not block much infrared light according to one source, so the back of the retina is being treated too. Clearly retinal tears and laser burns within the past day or two need to be getting infrared treatments before the cells die. Anyone else copying what I would do for myself assumes full responsibility for the results.
Retinal Safety Calculations
The ACGIH TLV safe dose for for the retina for green, yellow, red, and near infrared is anything that causes one of the following to be less than 1:
for 1 us to 10 seconds: 1/5000 * X * (width of source) / (distance to source) * seconds^0.25
The above is for 500 nm to 700 nm thermal only. I won't discuss blue light hazard which is a different topic. for 700 nm to 1050 nm multiply by 10^[(700-nm)/500]
for > 10 seconds: 1/600 * X * (width of source) / (distance to source)
this second one is based on a 7 mm pupil and a detector field of view of 11 mrad (i don't know what that means). At 10 seconds this seconds equation comes out about 8 times more dangerous than the first. There is another equation for cornea and leans safety, but it seems to be 10 or 100 times "safer" (less likely to affect cornea and lens) at less than 100 seconds, and many times more dangerous at 1000 seconds or greater (see previous comments). The "width/distance" is a factor that adjusts for smaller spots on the retina which are less dangerous because the heat can spread better to the sides of the retina, as long as the spot is less than 1.7 mm. If the spot is larger, this ratio is no longer has an effect. 1.7 mm spot is supposed to be 0.1 radians (source of light has a diameter 1/10th the distance to the eye), so that for ratios larger than 0.1, make the ratio a constant of 0.1 rather than further penalizing the source. However, I did not see where the ACGIH says this and even gives an example using 0.5 radians. So maybe the ratio is not meant to show small spots are safer, but to show larger spots are more dangerous.
The danger to the retina could be thermal burns that do not heal (blindness in spots) or maybe more floaters obscurring a little bit of vision from the internal fluid pulling away from retina a little more.
Example 5: (most dangerous red/infrared LED example)
For 10 seconds apply 1 Watt 660 nm or 630 nm LED outputing 75% of its 300 mW within +/- 20 degrees at 1 cm in front of pupil . Assume die area is 0.1x 0.1 = 0.01 cm^2 but that the focusing lens makes the die appear 5 times wider.
1/5,000 * 300 mW*0.75 / (4*pi (sin(20*2/4))^2) * 0.1*5 / 1 * 10^0.25 = 0.066 (supposedly safe by 1st calculation)
1/600 * 300 mW*0.75 / (4*pi (sin(20*2/4))^2) * 0.1 / 1 = 0.31 (supposedly safe, but not. See below)
If the angle of emission is +/-10 degrees, then multiply these numbers by a factor of 4, so the bottom is unsafe. Actually, since there is focusing into a small angle, the LED die will appear larger than it's actual 0.1 cm width, so these numbers are probably not safe (the 0.1 number should be larger, maybe 5 times larger).
Example 6: Typical 850 nm 5 mm LED safety.
Using data from example 1, hold a 850 nm LED 1 cm from pupil for MORE than 10 seconds: 1/600 * 2145 mW/cm^2/sr * sqrt(0.055) /1 = 0.82 This gives < 1 therefore supposedly safe for any length of time. Looking at the LED this "apparent die size after focusing" is not "contiguous" (there are gaps between the light) so that the retina may be able to dissipate the heat better than I'm implying, so it should be safer than this by a factor of about 3. Manufacturers may desire "contiguous" light from the focusing lens but this shows that is not desirable from a safety standpoint. An array of these will not be more dangerous than the individual LEDs, but simply affecting more spots, if it does have an effect. However, 5 mm LEDs can be run at 2 or 3 times than their ratings for 10 seconds without burning up. If they are kept cool with a fan they will still be efficient in turning the energy into light. So it is possible to run a 5 mm red or infrared LED in a way that it is not safe to look at it within a few cm of the eye. My guess is that it would be difficult for them to be harmful at more than 10 cm from the eye. LED Array: if the array is moved around in the field of vision, then the 2145 mW/cm^2/sr is effectively 10 times smaller as described in an example above, so arrays being moved around to treat the retina should be safe.
Example 7: Sun safety.
1 second staring at Sun. Sun insolation is 100 mW/cm^2 and is 0.53 degrees in the sky.
X = 100 * 1/pi * (distance to sun)^2 / (sun radius)^2 = 1,460,000 mW/cm^2/sr
Safety calculation: 1/5000 * X * 1.4E6/1.5E8 * 1^0.25 = 2.6 which is > 1.0 so it's risky even for a second if this is going to occur often in the work environment, not counting the UV and the much more dangerous blue light hazard.
Example 8:
Sun for > 10 seconds in one spot on eye: 1/600 * X * 1.4E6 / 1.5E8 = 23, very dangerours.
Lasers
are covered on other web pages, but here's the equation and calculation for comparison:
mW/cm^2 on retina = mW of laser / area of laser spot on retina = mW / (pi * (1/2 radian divergence of beam * eye focal length)^2.
Example 9: standard class IIIA, for presentations, 4 mW laser pointer, 0.001 rad divergence (I tested mine at 30 feet to confirm this):
mW/cm^2 on retina = 4 mW / (3.14*(0.0005*2.2)^2) = 1,760,000 mW/cm^2
This is 200 times more than the Sun. The only saving grace is that it is usually moving fast across the eye in a very small spot so that the tissue absorbs the 4mW heat energy. The small spot getting all the energy is the problem in the first place, but my point is that if it were as wide as the Sun (8 times wider), then it would not be 200 times more dangerous, but 8 times smaller is 200/8 = 25 times more dangerous, except the Sun has blue and UV which is the usual source of harm if you don't count life gaurds on white sand beaches who don't use sunglasses.
When the light beam is smaller than the pupil, the pupil radius is not in the equation.
The threshold retinal irradiances for just producing visible retinal lesions in the rhesus monkey eye were approximately 30 W cm^2 for 1 s, 23 W cm^2 for 10 s, 20 W cm^2 for 100 s, and 19 W cm^2 for 1,000 s (all for 500-um retinal spot diameters). This compares to only 0.03 W cm^2 for a 1,000-s exposure to 441-nm blue laser light (WHO 1982). Thermal retinal injury has been shown to dominate at wavelengths beyond 550 nm, and the threshold for thermal injury is retinal spot-size dependent because heat flow is more efficient for smaller diameter image sizes. The 500-um thresholds for thermal injury would be expected to be nearly twice the value for a 1,000-um (1-mm) image [1mm at same W/cm^2 is twice as dangerous because heat is not absorbed as well by surrounding tissue]. The 500-um image size corresponds to an angle of 29 mrad. For still larger retinal image sizes, this spot-size dependence becomes less, and by 1.7 mm diameter, the threshold is virtually a constant with increasing spot size. The 1.7-mm diameter retinal image is approximately 100 mrad [ 1.7 cm focal length * 0.1 rads incoming light = 1.7 mm spot on retina], and this is applied in guidelines to protect against thermal injury from both lasers and incoherent sources. Since the retinal irradiance is directly proportional to


Designers info
See also 850 verses 660 and safety. Customers will strap LED light therapy devices to their skin with ace bandages and under blankets and pillows and will leave them there all night and the heat can't be felt. Even 30 mW/cm^2 light output arrays can cause a 2nd degree burn if the heat can't escape. So an off timer like heating pads is required. LED viewing angle does not matter if the device is applied close to the skin. Don't forget blue LEDs will injure the retina, so use the widest angle lens as possible.Designers trying to select LEDs or arrays will have trouble comparing LED brightness from different manufacturers. The plastic encasings can focus the light and make mcd ratings much higher, but the amount of light coming out is the same. A 100 mcd LED at +/- 10 degrees (20 degrees angle of output) has the same total amount of light output as a 2,000 mcd LED at +/- 5 degrees (10 degrees). The equation is: Milliwatt output of an LED = mcd / (683 x P) x 2 x pi x (1-cos(1/2 Angle of output)). Companies are not exactly consistent in how they measure mcd (millicandela) and the angle output. Be careful in determining if they are stating 1/2 angle or full angle. P is the "photopic response factor" ( graph ) that depends on the wavelength. mcd and P are only meaningful for visible wavelengths (not infrared). P=1 for 555 nm and P=0.061 for 660 nm. For infrared, the measurement has to be mW/SR where SR=steradians. SR units are the percentage of a sphere's surface area, but divide SR by 4π (12.566) to get the percentage. SR is to a sphere as radians are to a circle. To convert from angle of output to steradians, use SR = 2 x pi x (1-cos(1/2 Angle of output)). Replace mcd/(683 x P) with mW/SR for infrared LEDs. In practice all this is not very useful. You just have to buy the LEDs and compare them. All 850 nm LED lamps I've tested had the exact same efficiency. As a rough estimate, the light output energy of an LED is 30% of the input energy. Strong LEDs use 50 to 100 mA continuously. But 20 mA red LEDs can put out enough light and are very common. A good and strong 850 nm LED will use 50 mA continuously, but the device will get too hot if you pack the LEDs closely (22 LEDs per square inch for 5 mm packages) and run them anywhere near their max. 0.8 watts per square inch is the maximum energy you can apply to any device that touches skin unless a fan or heat sink is used in order to the skin temperature below 105 F (FDA guideline). Kind of like a high fever on the skin, except the blood is able to take away the heat. So at a typical spacing of 12 LEDs per in^2 (2 LED per cm^2) you can apply 66 mW per LED. That's 45 mA at 1.55 V for the common 850 nm lamp and 35 mA at 1.9 V for a good 660 nm. LED spectrums can be generated with this spreadsheet.
Despite all the above, in directly measuring LED strength as described below, I measure only half the intensity reported by the datasheets. Datasheets report very roughly 1/3 of the energy input coming out as light output. I measure only half as much, about 18%. An expert on this tells me you can expect 15% to maybe 30% light ouput from LEDs used in light therapy.
You can measure the light intensity of anything in mW/cm^2 by using a styrofoam cup, cocoa powder, coffee or another water-blackening agent, and a home digital thermometer (accurate to 0.1 or 0.2 degrees C), based on the heat capacity of water. The equation is: W/cm^2 = 2cm x C x 4.18 / seconds where 2cm is the depth of water with dark cocoa powder to make it black water, C is increase in the water's temp, 4.18 is converting from calories to Joules, and seconds is the time the light was applied (200 seconds works best for high power device, up to 600 seconds for typical low power). The styrofoam cup needs to be cut off at 3 cm and LEDs can't be too close because air currents cause direct heating from the LEDs. For LED devices too small to cover the surface of the water, apply the light for longer amount of time and multiply the results by the water surface area divided by the surface area of the LED array. Do not take temp measurements in the sun or while the LED device is being applied because the metal absorbs the light and heats up. Water temp must be close to room temperature. For a simple red or infrared LED array running at about 30 mA per LED I get about 30 mW/cm^2 from 2.1 C rise after 10 minutes. My results are typically half of what LED manufacturer's data sheets say. I know the data sheets are wrong because their data is not usually self-consistent and my measurements of sun intensity are very accurate to the known intensity (100 mW/cm^2 when sun is > 80 degrees in the sky). The sky should be blocked from giviing light to the measurement cup bacuase reflections from the sky can provide 5 to 15% more light. To calculate sun intensity at any time at any location on a sunny day, use this spreadsheet.

Examples of Journal Articles
This is just a sampling that I haven't updated. The literature is too vast to review."But if the rats were treated with LED light with a wavelength of 670 nm for 105 seconds at 5, 25 and 50 hours after being dosed with methanol, they recovered 95 per cent of their sight. Remarkably, the retinas of these rats looked indistinguishable from those of normal rats. 'There was some tissue regeneration, and neurons, axons and dendrites may also be reconnecting,' says Whelan." "We believe that the use of NASA Light-Emitting Diodes (LED) for light therapy will greatly enhance the natural wound healing process, and more quickly return the soldiers to a pre-injury/ illness level of activity. The use of LED in combat with self-healing patches in future may enable the soldiers even after they are wounded to persist in combat better and longer." http://www.asc2002.com/Abstracts_only/d/DA-06.pdf
"LED produced improvement of greater than 40% in musculoskeletal training injuries in Navy SEAL team members, and decreased wound healing time in crew members aboard a U.S. Naval submarine. LED produced a 47% reduction in pain of children suffering from oral mucositis. CONCLUSION: We believe that the use of NASA LED for light therapy alone, and in conjunction with hyperbaric oxygen, will greatly enhance the natural wound healing process, and more quickly return the patient to a preinjury/illness level of activity. " "ATS treatments improve sensation in the feet of subjects with DPN, improve balance, and reduce pain."
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&dopt=Abstract&list_uids=11776448
"This technology may be the answer for problem wounds that are slow to heal....diabetic skin ulcers and other wounds in mice healed much faster when exposed to the special LEDs in the lab. Laboratory research has shown that the LEDs also grow human muscle and skin cells up to five times faster than normal...."
"Light close to and in the near-infrared range has documented benefits for promoting wound healing in human and animals. "
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&dopt=Abstract&list_uids=11568632
"ATS treatments improve sensation in the feet of subjects with diabetic peripheral neuropathy, improve balance, and reduce pain."
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&list_uids=14693984
"Near-infrared irradiation potentially enhances the wound healing process, presumably by its biostimulatory effects."
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&list_uids=11722751
" It was found that laser exposure resulted in more pronounced restoration of functional state of nervous fibers than conventional therapy. Application of laser irradiation of low intensiveness was effective while in combined therapy of distal diabetic polyneuropathy as well as monotherapy."
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&list_uids=9677693
"exposure of volunteers to visible and infrared polarized (VIP) light leads to a fast increase in the growth promoting (GP) activity of the entire circulating blood for human KCs in vitro, which is a consequence of the transcutaneous photomodification of blood and its effect on the rest of the circulating blood volume."
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&list_uids=14743286
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&list_uids=14521091
"The method of monochromatic near infrared stimulation can be used for selective stimulation of several regions of the external auditory canal,.."
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&list_uids=14999583
LED and LLL irradiation resulted in an increased fibroblast proliferation in vitro. This study therefore postulates possible stimulatory effects on wound healing in vivo at the applied dosimetric parameters.
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&list_uids=12928819
Wound healing was significantly more rapid with than without FIR. Skin blood flow and skin temperature did not change significantly before or during far-infrared irradiation.
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=pubmed&list_uids=12773705
Although more studies are needed, LED therapy appears useful in the prevention of OM in pediatric BMT patients.
http://www.ncbi.nlm.nih.gov/entrez/query.fcgi
News articles on the NASA Study:
http://garm.dyndns.org/whelan_lab/01/html/%20/whelan.html
http://www1.msfc.nasa.gov/NEWSROOM/news/releases/2000/00-336.html
http://healthlink.mcw.edu/article/975450257.html
http://www.hypography.com/article.cfm?id=29173
http://www.viahealth.org/via_news/news2002/april/woundstudy.htm
http://www.engr.wisc.edu/industry/atwork/vol5/WCSAR.html
http://www.scienceblog.com/community/older/archives/D/archnas202.html
A wound-healing device was placed on the USS Salt Lake City submarine, and doctors reported 50 percent faster healing of crewmember's lacerations when exposed to the LED light. Injuries treated with the LEDs healed in seven days, while untreated injuries took 14 days.
second daily infrared (JR) laser (820 nm, 25mW) and visible red laser (670 nm, 10 mW) at 1 J/cm2 and 5 J/cm2 on chronic pain. ...five treatment sessions over a two-week period. ...significant reductions in pain over the duration of the study with those groups which received infrared (820nm) laser a 1 J/cm2 and 5 J/cm2
904 nm three times weekly for 2 weeks, ......tendonitis of the shoulder
3.5-inch by 4.5-inch (89-millimeter by 114-millimeter), portable flat array of LEDs, arranged in rows on the top of a small box. ......places the box of LEDs on the outside of the patient's cheek about one minute each day. The red light penetrates to the inside of the mouth, where it seems to promote wound healing and prevent further sores in the patient's mouth.
All 176 patients received six treatments during a period of 3-4 weeks. ..GAAs laser therapy for tendinitis and myofascial pain
A 40 year-old woman presented at the Abe Orthopedic Clinic with a 2-year history of lower back pain and pain in the left hip and leg diagnosed as a ruptured disc between the 5th lumbar/1st sacral vertebrae. .....The gallium aluminum arsenide (GaAlAs) diode laser (830 nm, 60 mW) was used in outpatient therapy, and after 7 months, the patient's condition had dramatically improved, demonstrated by motility exercises. This improvement was confirmed by further MRI scans, which showed clearly the normal condition of the previously herniated L5/SI disc.
Influence of low-level (810nm, GaAlAs semiconductor) laser on bone and cartilage during joint immobilization was examined with rats' knee model. .......The hind limbs of 42 young Wistar rats were operated on in order to immobilize the knee joint. One week after operation they were assigned to three groups: irradiance 3.9W/cm2, 5.8W/cm2, and sham treatment. After 6 times of treatment for another 2 weeks both hind legs were
myofascial pain in the cervical region. The patients were submitted to 12 sessions on alternate days to a total energy dose of 5 J each.
RA:From July 1988 to June 1990, 170 patients with a total of 411 affected joints were treated using a GaAlAs diode laser system (830 nm, 60 Mw C/W). Patients mean age was 61 years
890 nanometer (nm)....Venous ulcers, diabetic ulcers, and post-amputation wounds....It recently has been demonstrated that application of this particular MIRE device to the skin for 30 minutes increases plasma NO in nondiabetic subject volunteers, as measured with a Sievers Instrument, Model 280, Nitric Oxide Detector
© 2004-2012 heelspurs.com LLC
Author: Scott Roberts
scott@heelspurs.co
Subscribe to:
Posts (Atom)